Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 100

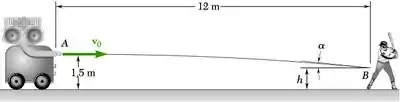
Uma máquina que lança bolas de beisebol a uma velocidade horizontal v0. Sabendo que a altura h varia entre 0,8 m e 1 m, determine (a) o intervalo de valores de v0, (b) os valores de α correspondentes a h = 0,8 m e h = 1 m

Passo 1

  1. Movimento vertical. (Movimento uniformemente acelerado)

    2. y = 0 + 0 t - 1 2 g t 2

    Movimento horizontal. (Uniforme)

    x = 0 + v x 0 t = v 0 t

    Quando h = 31 in., y = - 2 5 12   ft :

    - 2 5 12   ft = - 1 2 32.2   ft/ s 2 t 2

    ou

    t 31 = 0.387432   s

    Então

    40   ft = ( v 0 ) 31 0.387432   s

    ou

    ( v 0 ) 31 = 103.244   ft/s = 70.4   mi/h

    Quando h = 42 in., y = - 1.5   ft :

    - 1.5   ft = - 1 2 32.2   ft/ s 2 t 2

    ou

    t 42 = 0.305234   s

    Então

    40   f t = ( v 0 ) 42 0.305234   s

    ou

    ( v 0 ) 42 = 131.047   ft/s   = 89.4   mi/h

    Passo 2

  2. Para o movimento vertical

v y = 0 - g t

Agora

tan ⁡ α = v y B v x B = g t v 0

Quando h = 31 in.:

tan ⁡ α = 32.2   ft/ s 2 0.387432   s 103.244   ft/s

= 0.120833

Quando h = 42 in.:

tan ⁡ α = 32.2   ft/ s 2 0.305234   s 131.047   ft/s

= 0.07500

Resposta

a )   70.4   mi/h ≤ v 0 ≤ 89.4   ft/s

b )   a 31 = 6.89 °

α 42 = 4.29 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que a velocidade do bloco B com relação ao bloco A é vB/A 5,6 m/s ∡ 70°, determine as velocidades de A e B.
Determine o menor raio que deveria ser usado para a rodovia se a componente normal da aceleração do carro viajando a 72 km/h não pudesse exceder 0,7 m/s² .
O pino A, que está fixado à haste de conexão AB, tem seu movimento restrito à ranhura circular CD. Sabendo que no instante t = 0 o pino parte do repouso e se movimenta de tal modo que sua velocidade e
Uma pista ao ar livre tem 125 m de diâmetro. A corredora aumenta sua velocidade escalar numa taxa constante de 4 para 7 m/s em uma distância de 28 m. Determine a aceleração total da corredora 2 s depo
Um trem monotrilho parte do repouso em uma curva de raio 400 m e acelera com uma taxa constante a1 . Se a aceleração máxima total do trem não deve exceder 1,5 m/s² , determine (a) a distância mais cur