Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 137
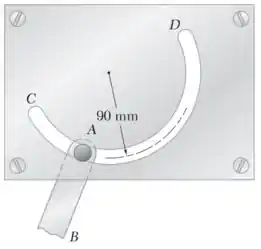
O pino A, que está fixado à haste de conexão AB, tem seu movimento restrito à ranhura circular CD. Sabendo que no instante t = 0 o pino parte do repouso e se movimenta de tal modo que sua velocidade escalar aumenta a uma taxa constante de 20 mm/s² , determine a intensidade da aceleração total quando (a) t - 0 e (b) t - 2 s.
Passo 1
(a)Em t=0, = 0, o que implica
ou
Passo 2
(b)Nós temos um movimento de aceleração uniforme
Em t = 2s:
Agora
Finalmente
ou
ou
Resposta
Exercícios de Livros Relacionados
Em um determinado instante, o caixote de 40k g tem uma velocidade de 10m / s subindo o plano inclinado a 20 ° . Calcule o tempo t necessário para o caixote atingir o repouso e a correspondente distânc
Calcule a aceleração vertical a do cilindro de 150k g para cada um dos dois casos ilustrados. Despreze o atrito e a massa de polias.
Um carro A viaja a uma velocidade constante de 100k m / h . Quando na posição mostrada no instante de tempo t = 0 , o carro B tem uma velocidade de 40k m / h e acelera a uma taxa constante de 0,1 g ao
Repita o Prob. 2/59, salvo que o carro B , em vez de possuir uma aceleração constante, agora acelera conforme mostrado no gráfico a seguir. O instante de tempo t 2 é o momento em que a velocidade perm
Despreze completamente o atrito e a massa das polias e determine as acelerações dos corpos A e B após a liberação a partir do repouso.