Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 60

O sistema mostrado parte do repouso e o comprimento da corda superior está ajustado para que A, B e C estejam inicialmente no mesmo nível. Cada componente se move com uma aceleração constante e, depois de 2 s , a variação da posição relativa do bloco C em relação ao bloco A é de 280 m m .

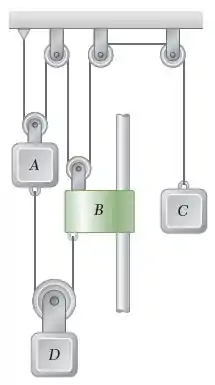
Passo 1

Cabo (1): 2 y A + 2 y B + y C = c o n s t a n t e

Então 2 v A + 2 v B + v C = 0

E 2 a A + 2 a B + a C = 0

Cabo 2: y D - y A + y D - y B = c o n s t a n t e

Então - v A - v B + 2 v D = 0

E - a A - a B + 2 a D = 0

Dado: em t = 0 ,   v = 0 ; todas as acelerações constantes;

( y A ) 0 = ( y B ) 0 = ( y C ) 0

Todas as acelerações em t = 2 s

y C / A = 280 m m ↑

Quando v B / A = 80 m m / s ↓

y A - y A 0 = 160 m m ↑ y B - y B 0 = 320 m m ↓ a B > 10 m m / s ²

Passo 2

  1. Temos: y A = y A 0 + 0 t + 1 2 a A t ²

E y C = y C 0 + 0 t + 1 2 a C t ²

Então y C / A = y C - y A = 1 2   x   a C - a A t ²

Em t = 2 s ,   y C / A = - 280 m m :

- 280 m m = 1 2   x   a C - a A   x   2 s 2

Ou a C = a A - 140

Substituindo em Eq.(2)

2 a A + 2 a B + a A - 140 = 0

Ou a A = 1 3   x   ( 140 - 2 a B )

Agora v B = 0 + a B t v A 0 + a A t v B / A = v B - v A = a B - a A t

Passo 3

Além disso y B = ( y B ) 0 + 0 t + 1 2 a B t ²

Quando v B / A = 80 m m / s ↓ : 80 = a B - a A t

∆ y A = 160 m m ↓ : 160 = 1 2 a A t ²

∆ y B = 320 m m ↓ : 320 = 1 2 a B t ²

Então 160 = 1 2   x   a B - a A t ²

Usando Eq.(7) 320 = 80 t       o u     t = 4 s

Então 160 = 1 2 a A   x   ( 4 ) ²

E 320 = 1 2 a B   x   ( 4 ) ²

Observe que E1. (6) não é usado; assim, o problema está sobre determinado.

Resposta

  1. a A = 20 m m / s ² ↓

a B = 40 m m / s ² ↓

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um projétil é disparado a partir do ponto A com uma velocidade inicial v0. (a) Mostre que o raio de curvatura da trajetória do projétil alcança seu valor mínimo no ponto mais alto B da trajetória. (b)
Uma criança lança uma bola do ponto A com velocidade inicial vA de 20 m/s com um ângulo de 25° em relação à horizontal. Determine a velocidade da bola nos pontos da trajetória descrita pela bola onde
Uma tubulação horizontal descarrega no ponto A um jato de água dentro de um reservatório. Determine o raio de curvatura do jato no ponto B em termos das intensidades das velocidades vA e vB.
Em um dado instante de uma corrida de aeronaves, o avião A está voando horizontalmente em linha reta e sua velocidade escalar aumentada a uma taxa de 8 m/s2 . O avião B está voando na mesma altitude q
Uma bola de basquete é solta no chão no ponto A e quica com velocidade vA de intensidade 2,25 m/s como mostrado na figura. Determine o raio de curvatura da trajetória descrita pela bola (a) no ponto A