Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 122

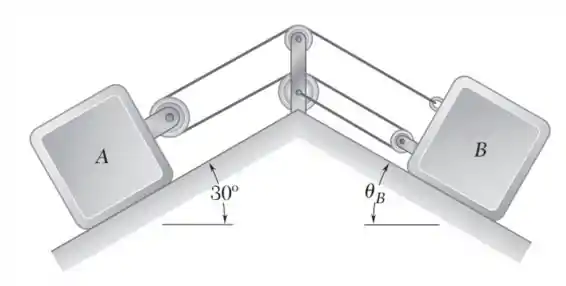
Sabendo que a velocidade do bloco B com relação ao bloco A é vB/A 5,6 m/s ∡ 70°, determine as velocidades de A e B.

Passo 1

Do diagrama

2 v A + 3 v B = c o n s t a n t e

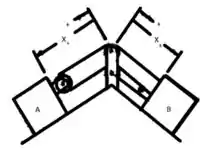
Então

2 v A + 3 v B = 0

ou

v B = 2 3 v A

Agora

v B = v A + v B / A

Passo 2

e notando que v A e v B devem ser paralelos a superficie A e B, respectivamente, a representação gráfica da equação é a mostrada. Nota: Assumindo que v A é direcionada para cima da inclinação leva a um diagrama de velocidade que não “fecha”.

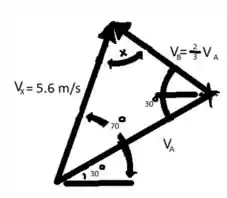
Primeiro notamos

α = 180 ° - ( 40 ° + 30 ° + θ B )

= 110 ° - θ B

Então

v A s e n 110 ° - θ B = 2 3 v A s e n 40 ° = 5.6 s e n 30 ° + θ B

v A s e n 40 ° = 2 3 v A s e n 110 ° - θ B

s e n 110 ° - θ B = 0.96418

θ B = 35.3817 °

e

θ B = 4.6183 °

Para θ B = 35.3817 ° :

v B = 2 3 v A = 5.6   s e n 40 ° s e n 30 ° + 35.3817 °

ou

v A = 5.94 m / s       v B = 3.96 m / s

Passo 3

Para θ B = 4.6183 ° :

v B = 2 3 v A = 5.6   s e n 40 ° s e n 30 ° + 4.6183 °

ou

v A = 9.50 m / s       v B = 6.34 m / s

Resposta

Para θ B = 35.3817 ° :

v A = 5.94 m / s   ∡ 30 °

v B = 3.96 m / s     ∡ 35.4 °

Para θ B = 4.6183 ° :

v A = 9.50 m / s   ∡ 30 °

v B = 6.34 m / s     ∡ 4.62 ° ,

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante t = 0 uma pequena bola é arremessada a partir do ponto A com uma velocidade de 60m / s no ângulo de 60 ° . Despreze a resistência atmosférica e determine os dois instantes de tempo t 1 e t
Uma pedra é lançada para baixo de uma encosta como mostrado. Determine o módulo u e a direção θ da sua velocidade inicial de modo que a pedra suba 12m e ainda tenha um alcance de 50 metros para baixo
Logo após ter sido atingida por um taco, uma bola de golfe tem uma velocidade de 38m / s direcionada a 35 ° com a horizontal conforme apresentado. Determine a localização do ponto de impacto.
Durante um teste de frenagem, o carro com motor traseiro é parado a partir de uma velocidade inicial de 100k m / h em uma distância de 50m . Se é sabido que todas as quatro rodas contribuem igualmente
O caixote de 50k g está parado quando a força P é aplicada. Determine a aceleração resultante do caixote se (a) P = 0 , (b) P = 150N e (c) P = 300N .