Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 103
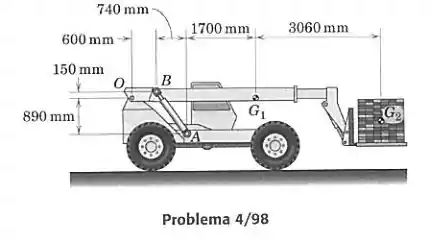
A máquina mostrada é usada para mover itens pesados, tal como estrados de tijolos, em locais de construção. Para a posição horizontal mostrada da lança, determine a força em cada um dos dois cilindros hidráulicos . A massa da lança é de 1500 kg, com centro de massa em , e a massa do cubo de tijolos é de 200 kg, com centro de massa em .
Passo 1
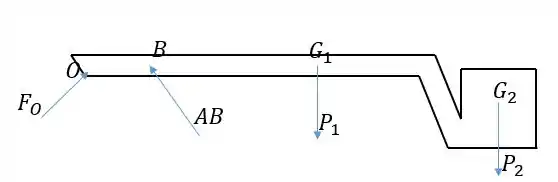
Vamos isolar a lança e os tijolos em conjunto em um diagrama de corpo livre. Como há um cilindro hidráulico de cada lado, a força feita por cada um é igual e devemos dividir por dois no final.
Passo 2
Podemos encontrar diretamente fazendo o momento em torno de , pois esta é a única incógnita. Só precisamos antes calcular o valor dos pesos e o ângulo que faz com a horizontal. Para os pesos, temos:
Calculamos o ângulo que faz com a horizontal através de sua tangente, dada pelas distâncias no desenho do enunciado:
Passo 3
Agora podemos fazer o momento em torno de . Devemos notar que as componentes vertical e horizontal de causam momento nesse ponto, pois há uma pequena diferença de altura de 150 mm entre e . As distâncias horizontais de até e são:
Então:
Agora dividimos por 2 e encontramos a força feita por cada cilindro: