Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 232

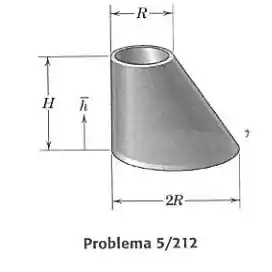
A figura mostra um corpo semelhante ao do Prob. 5/211, mas agora o corpo é uma casca fina com aberturas na base e no topo. Determine a altura h - de seu centro de massa, acima da base do sólido homogêneo, e compare seu resultado com a resposta para o Prob. 5/211.

Passo 1

A fórmula da coordenada z - do centro de massa de uma casca homogênea é:

z - = ∫ z   d A ∫ d A

Então devemos resolver as duas integrais e acharemos o valor de h - = z - .

Passo 2

Primeiro vamos calcular a área A = ∫ d A . Assim como no Prob. 5/211, temos um raio em função da altura z dado por r z = 2 R - R H z . Então a área de uma circinferência fina de altura d z é:

d A = 2 π r z d z = 2 π 2 R - R H z d z

Integrando de 0 a H , vamos obter a área:

A = ∫ d A = ∫ 0 H 2 π 2 R - R H z d z = 2 π 2 R z - R 2 H z 2 0 H

= 2 π 2 R H - R 2 H H 2 = 4 π R H - π R H = 3 π R H

Passo 3

Agora vamos calcular ∫ z   d A :

∫ z   d A = ∫ 0 H 2 π z 2 R - R H z d z = ∫ 0 H 2 π 2 R z - R H z 2 d z

= 2 π R z 2 - R 3 H z 3 0 H = 2 π R H 2 - R H 2 3

= 2 π ⋅ 2 R H 2 3 = 4 3 π R H 2

Passo 4

Só falta dividir as duas integrais e chegamos no resultado:

h - = z - = ∫ z   d A ∫ d A = 4 3 π R H 2 3 π R H = 4 9 H

O centro de massa da casca fica mais próximo da altura H 2 que no caso do corpo sólido, o que é esperado pois o peso de cada altura depende linearmente de z na integral, enquanto para o corpo sólido depende de z 2 , o que faz com que tenha mais concentração de massa na parte de baixo.

Resposta

h - = 4 9 H

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2- Faça com seu lápis um ponto sobre a posição da sua melhor estimativa visual do centroide da área do setor circular. Verifique sua estimativa usando os resultados do Exercício 5/3.
Localize o centroide da área sombreada entre as duas curvas.
Determine a coordenada y do centroide da área sombreada
A espessura da placa triangular varia linearmente em y, dede o valor t 0 ao longo da sua base em y = 0 até 2 t 0 em y = h. Determine a coordenada y do centro de massa da placa.
Localize o centroide da área mostrada na figura por integração direta. (Cuidado: Observe cuidadosamente o sinal correto da raiz envolvida.)