Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 70
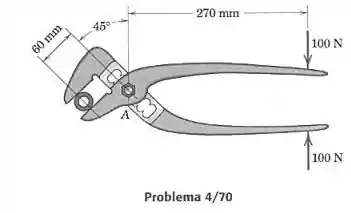
Calcule a força suportada pelo pino em para o alicate com junta deslizante sob um aperto de 100 N.
Passo 1
Primeiro devemos separar as duas partes do alicate em diagramas do corpo livre. Consideramos o pino A e o objeto redondo que está sendo comprimido como parte de um dos corpos. Temos que prestar atenção nas forças de ação e reação entre as 3 partes.
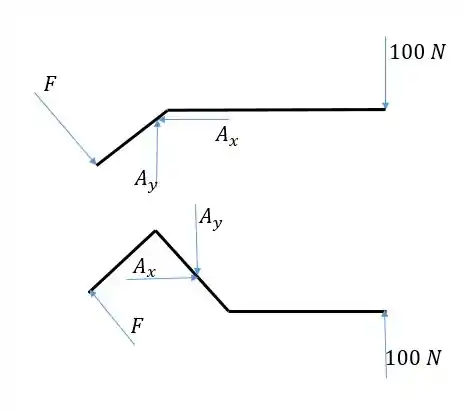
Passo 2
Vamos usar a parte de cima. Agora devemos aplicar as equações de equilíbrio para os corpos para encontrarmos e . Fazendo o momento em torno de , encontramos a força :
Agora fazendo a soma das forças horizontais, encontramos :
Fazemos a soma das forças em para encontrar :
Passo 3
Então só falta encontrar o modulo da força:
Resposta
Exercícios de Livros Relacionados
3.17. Os vetores P e Q constituem dois lados adjacentes de um paralelogramo. Determine a área do paralelogramo quando (a) P =- 7î + 3j ^ - 3k ^ î e Q = 2î + 2j ^ + 5k ^ î , (b) P = 6î - 5j ^ - 2k ^ î
3.19. Determine o momento em relação à origem O da força F = 4î + 5j ^ + 3k ^ î que atua em um ponto A. Suponha que o vetor posição de A seja (a) r = 2î - 3j ^ + 4k ^ î , (b) r = 2î + 2,5j ^ - 1,5k ^
3.20. Determine o momento em relação à origem O da força F = - 2î + 3j ^ + 5k ^ î que atua em um ponto A. Suponha que o vetor posição de A seja (a) r =î + j ^ +k ^ î , (b) r = 2î + 3j ^ - 5k ^ î , (c)
23- Uma barra de 6m tem um ponta fixada em A . Um cabo de aço é esticado da ponta livre B da barra ao ponto C localizado na parede vertical. Se a tensão no cabo é 2.5k N , determine o binário que a fo
32- No Problema 3.25 determine a distância perpendicular do ponto A até uma linha que passa pelos pontos C e G .