Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas Fundamentais - Ex. 5
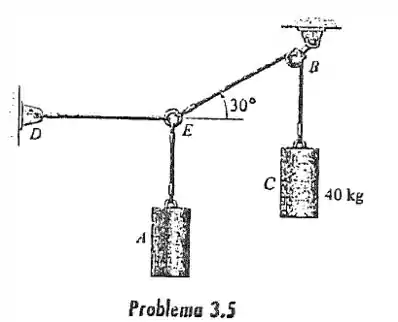
Se a massa do cilindro C é 40 kg, determine a massa do cilindro A, de modo a manter a montagem na posição mostrada.
Passo 1
Fala!
Para esse exercício devemos analisar o diagrama de corpo livre, da argola em e na rótula em :
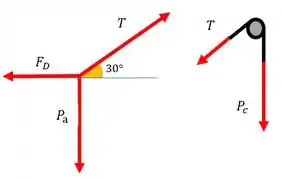
Perce que é a força no cabo que suporta o peso do latão em C. Pelo equilíbrio, a tensão nas duas extremidades desse cabo devem ser iguais, logo
Aí a gente pode achar pelo equilíbrio de forças no ponto E. Bora!
Passo 2
Como o bloco não se mexe, a soma de forças em e em deve ser zero. Perceba que em existe uma força que não nos importa descobrir, então não precisamos analisar esse eixo nessa questão.
A soma das forças em são:
Percebe que a gente achou a componente em de para usar no somatório.
O peso de um objeto é igual a massa dele, vezes a gravidade, então
Podemos dividir tudo por
Nós conhecemos o ângulo e a massa , substituindo: