Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 103
Determine a expressão para a intensidade do binário M que deve ser aplicado para equilíbrio.
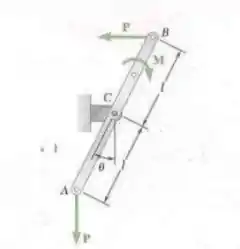
Passo 1
Fala aí galera, vamos para mais um problema de estática. Este problema é bem simples, só temos que decompor as distâncias de P até o ponto de interesse em função dos ângulos. Para isso, vamos aplicar as equações de equilíbrio:
Logo, isolando M:
A força será:
Resposta
Exercícios de Livros Relacionados
Se a corda AB de 1,5 m pode suportar uma força máxima de 3500 N, determine a força na corda BC e a distância y, de modo que a caixa de 200 kg possa ser suportada.
Determine o comprimento não esticado de DB para manter o caixote de 40 kg na posição mostrada. Considere k = 180 N/m.
Determine a força em cada cabo e a força F necessária para manter a luminária de 4 kg na posição mostrada. Dica: primeiro analise o equilíbrio em B; depois, usando o resultado para a força em BC, anal
Duas esferas, A e B, têm massas iguais e estão eletrostaticamente carregadas, de modo que a força repulsiva que atua entre elas tem uma intensidade de 20 mN e está direcionada ao longo da linha AB. De
As molas BA e BC possuem uma rigidez de 500 N/m cada e um comprimento não esticado de 3 m. Determine o deslocamento d da corda a partir da parede quando uma força F = 175 N é aplicada à corda.