Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 10
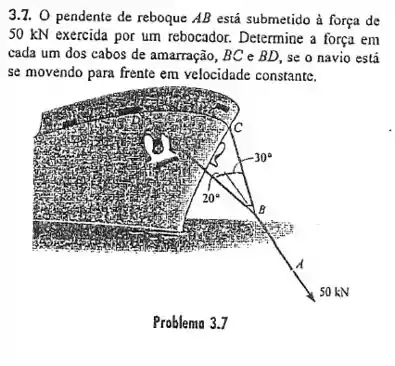
Passo 1
Se o navio se move para frente com uma velocidade constante o nó também ira se mover dessa forma. Quando um corpo temuma velocidade constante significa que sua aceleração é igual a zero, ou seja, o somatório das forças que atuam nesse corpo é igual a zero.
Então vamos fazer o diagrama de corpo livre desse nó para calcularmos as intensidades das forças nos cabos BC e BD:
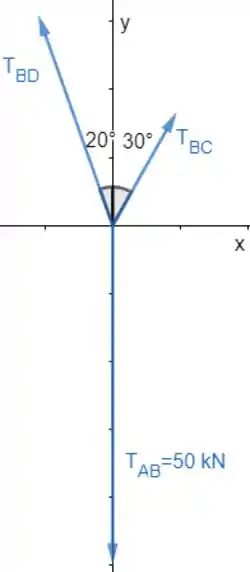
Passo 2
A soma de forças em e em deve ser zero.
Vamos decompor primeiro as forças em :
Passo 3
Agora vamos decompor as forças em para achar a força :
Nós descobrimos no passo anterior o valor de vamos usa-lo nesse equação:
Seno sobre cosseno é igual a tangente, então cosseno sobre seno é 1 sobre a tangente:
Passo 4
Agora que temos vamos usar a equação que achamos no Passo 2 para descobrir
Resposta
Exercícios de Livros Relacionados
Para o sistema e o carregamento mostrados na figura, determine a a força P necessária para o equilíbrio, b a força correspondente no elemento B D , c a reação correspondente em C .
Uma força P de intensidade 16 k N é aplicada no pistão do motor mostrado na figura. Para cada uma das duas posições mostradas, determine o binário M necessário para manter o sistema em equilíbrio.
O pino em B é fixado ao elemento A B C e pode deslizar livremente ao longo do rasgo aberto na placa fixa. Desconsiderando o efeito do atrito, determine o binário M necessário para manter o sistema em
O braço A B C está ligado por pinos ao colar em B e à manivela C D em C . Desprezando o efeito do atrito, determine o binário M necessário para manter o sistema em equilíbrio quando θ = 90 ° .
O pino em B é fixado ao elemento A B C e pode deslizar livremente ao longo do rasgo aberto na placa fixa. Desconsiderando o efeito do atrito, determine o binário M necessário para manter o sistema em