Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 111
A massa total do cabo é . Considerando que a massa do cabo distribuída uniformente ao longo da horizontal. Determine a flecha e a inclinação do cabo entre e .
Passo 1
Bom galera, vamos começar esboçando o cabo pra facilitar nossa vida, fica mais ou menos assim:
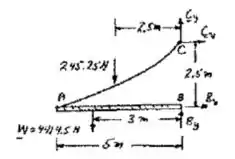
Assim, lembrando que o corpo está em equilíbrio, temos:
Então, encontramos:
Passo 2
Show de bola, também podemos analisar apenas o cabo, bem assim:
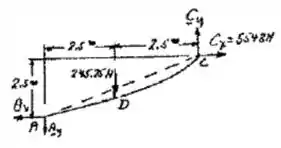
Onde:
E quanto ao momento fica:
Resolvendo essa equação encontramos:
Passo 3
Agora, a gente já pode encontrar os ângulos, pra isso basta a gente usar a função inversa da tangente.
Vamos primeiro calcular o ângulo no ponto :
E no ponto fica:
Passo 4
Por fim, vamos encontrar a flecha , para isso a gente vai usar o somatório dos momentos sabendo que o corpo encontrasse em equilíbrio:
Vamos então pegar apenas a metade do cabo (De até ).
Então, agora fica fácil né?
Ou seja: