Dois cabos de igual bitola são presos a uma torre de transmissão em . Como a torre é estreita, o componente horizontal da resultante das forças exercidas pelos cabos em deve ser nulo. Sabendo que a massa por unidade de comprimento dos cabos é , determine (a) a flecha necessária , (b) a tração máxima em cada cabo.
Passo 1
Bom galera, vamos começar esboçando o cabo pra facilitar nossa vida, fica mais ou menos assim:
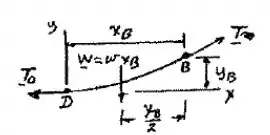
Assim, lembrando que o corpo está em equilíbrio, temos:
Logo a componente horizontal é dada por:
Passo 2
Show de bola, como de até mede , a gente tem que é igual a metade disso, logo:
Com isso a gente consegue encontrar aquela componente horizontal do passo anterior:
Já no cabo de até , ficamos com:
Igualando os dos dois cabos:
Encontramos:
Passo 3
Por fim, temos que encontrar a tensão máxima, para isso a gente vai usar pitágoras com a componente máxima horizontal e a componente máxima vertical, bem assim:
Primeiro encontramos esses termos no cabo :
Fazendo pitágoras ficamos com:
E fazendo o mesmo que acabamos de fazer, mas agora no cabo , encontramos: