O cabo sustenta uma carga uniformemente distribuida ao longo da horizontal, como mostra a figura. Sabendo que em o cabo forma um ângulo com a horizontal, determine (a) a máxima tensão no cabo, (b) a distância vertical de até o ponto mais baixo do cabo.
Passo 1
Bom galera, vamos começar esboçando o cabo pra facilitar pra gente:
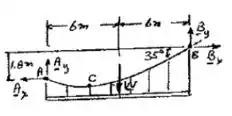
Logo:
E o peso é bem fácinho, apenas essa continha simples:
Passo 2
Show de bola, agora vamos dar uma analisada marota no momento, pra isso vamos adotar o ponto como eixo de rotação:
Resolvendo isso encontramos:
E com isso a gente já pode encontrar também:
Passo 3
Agora, vamos analisar apenas a parte , primeiro o esboço:
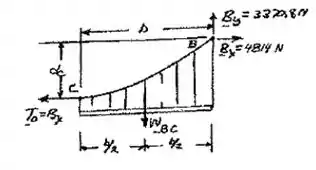
E ao analisarmos as forças no eixo vertical, sabendo que o corpo está em equilíbrio fica:
Logo:
Então, a gente usa a formula do peso:
Passo 4
Por fim, a gente já tem as informações para analisar o momento da parte , e vamos usar o ponto como eixo de rotação para isso:
Resolvendo essa equação, encontramos:
Agora tá fácil demais, né?
E a tração máxima bastar usar Pitágoras rapidinho, assim: