Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 141
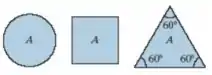
O material de fabricação de cada um dos três eixos tem tensão de escoamento e módulo de cisalhamento . Determine qual das geometrias resistirá ao maior torque sem escoamento. Qual porcentagem desse torque pode ser suportada pelos ouros eixos? Considere que cada eixo é feito com a mesma quantidade de material e a mesma área de seção transversal.
Passo 1
Falaa!
A questão quer que a gente analise qual dessas formas resiste melhor à torção. As únicas informações das questão são: a área igual das três figuras e que elas tem a mesma tensão de escoamento.
A estratégia de resolução é a seguinte: Vamos tentar utilizar as equações da Tabela 5.1 para fazer essa análise porque elas dão a tensão de cisalhamento em relação ao torque para seções nesses formatos. São elas:
- Para um quadrado de lado :
- Para o triângulo de lado a:
- Para o círculo de raio :
Repara que a gente quer o , tem , mas não tem as dimensões das seções, só sabemos que elas tem áreas iguas.
Vamos aproveitar que as três formas tem áreas iguais de valor para relacionar o lado do quadrado, com o lado do triângulo e o raio da circunferência. Bora!
Passo 2
Vamos achar as dimensões das nossa peças em função de a área comum a elas.
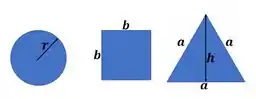
Vamos relacionar a área do triângulo com o lado, sabendo que todos os ângulos internos dele vale :
Área da circunferência:
Área do quadrado:
Passo 3
Agora vamo utilizar as equações da Tabela 5.1 para calcular os torques:
Quadrado:
Triângulo:
Círculo:
Passo 4
Baseado nas equações anteriores, percebemos que a estrutura que aguenta maior torque é a circunferência.
Vamos agora dividir o torque no triângulo e o torque no quadrado pelo torque máximo, para encontrar as razões entre eles.
Porcentagem do torque sobre a seção quadrada
Porcentagem do torque sobre a seção triangular
Resposta
A que aguenta mais é a seção circular.