Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 138
O eixo cônico é feito de liga de alumínio 2014-T6 e seu raio pode ser descrito pela função , onde é dado em metros. Determine o ângulo de torção de sua extremidade A se ele for submetido a um torque de
Passo 1
A questão nos fornece os dados: e nos pede a deformação no ponto A:
Para resolver a questão temos que aplicar a equação da deformação. Mas como a barra não é linear, a equação só é válida para deformações infinitesimais:
Passo 2
Na equação da deformação, apenas o torque e o coeficiente de cisalhamento são constantes. O momento de inércia é uma função de porque o raio varia com a distância:
Passo 3
Aplicamos agora a equação da deformação:
Substituímos nela a equação do momento de inércia:
Agora integramos os dois lados. Os limites de integração são do ínicio ao fim do eixo:
Passo 4
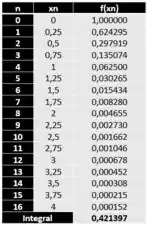
A integral acima não é trivial, e é mais facilmente resolvida numericamente:
Usando a regra dos trapézios, com um passo de
Passo 5
Aplicando o resultado na equação da deformação: