Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 127
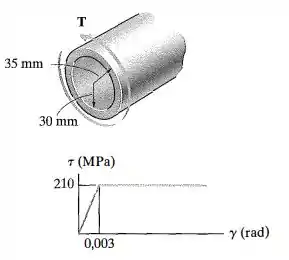
O tubo de de comprimento é feito de um material elástico perfeitamente plástico como mostra a figura. Determine o torque aplicado T que submete o material da borda externa do tubo à deformação por cisalhamento Qual será o ângulo de torção permanente do tubo quando esse torque for removido? Faça um rascunho da distribuição de tensão residual no tubo.
Passo 1
Dados da questão: e o material é elástico perfeitamente plástico.
A questão pede:
- O torque (precisaremos descobrir se o torque é plástico ou elasto-plastico)
- O ângulo de torção residual (permanente)
Estratégia de resolução:
- Primeiro, precisamos saber se há ou não núcleo elástico nessa torção. Em outras palavras, precisamos saber se o raio interno está em regime plástico ou elástico.
- Podemos, então aplicar a equação 5.23 para determinar o torque, com atenção ao tipo de regime de tensão atua.
- Utilizando a deformação fornecida pela questão podemos calcular o ângulo de torção plástica
- Utilizando o torque poderemos calcular o ângulo de recuperação de torção elástica.
- Por fim vamos calcular o ângulo de torção residual
Passo 2
Em questões que envolvem deformação permanente, será útil sabermos o valor do momento de inércia e do módulo de cisalhamento do material
Momento de inércia:
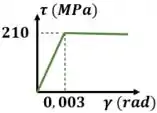
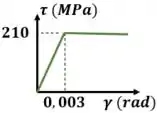
O módulo de cisalhamento pode ser calculado observando o gráfico fornecido e utilizando a lei de hook:
Passo 3
Para saber se há ou não região de comportamento elástico basta calcular qual é a deformação na região interna do eixo.
Por proporção, sabemos que:
Manipulando:
Substituíndo os valores:
A deformação é maior do que a deformação de escoamento. Isso quer dizer que toda a seção transversal tem comportamento plástico.
Passo 4
Agora aplicamos a Equação 5.23 para determinar o torque:
Observando o gráfico fornecido, sabemos que no regime plástico a tensão é constante e igual a tensão de escoamento.
Substituíndo os valores:
Passo 5
Para determinar o ângulo de torção permanente primeiro precisamos saber qual foi o ângulo de torção gerado pela deformação plástica. Pela equação 5.25
Substituíndo os valores:
Passo 6
Quando o torque é removido, o material recupera parte do seu formato original. Para calcular, basta aplicar o mesmo torque, mas considerando um regime elástico (afinal, é uma “recuperação elástica”). Podemos aplicar a equação 5.15:
Substituíndo os valores:
Passo 7
Para terminar a questão, basta subtrair a o ângulo de recuperação elástica do ângulo de deformação plástico e encontramos o ângulo de torção residual.
Substituíndo os valores