Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 214

Para o mecanismo do problema indicado nas figuras, determine a aceleração do colar A.

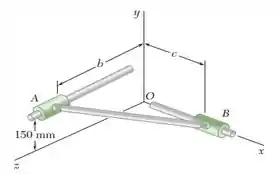
Passo 1

E ai gurizada tudo belezinha???

Geometria: c = 0.175   m ,                     l A B = 0.275 m

l A B 2 = c 2 + 0.150 2 + b 2         o u           0.275 2 = 0.175 2 + 0.15 2 + b 2

b = 0.15   m

r A / B = - 0.175   m i + 0.15   m j + 0.15   m k

Velocidade no colar B: v B = - ( 180   m m / s ) i = - ( 0.18   m / s ) i

Passo 2

Velocidade do colar A: v A = v A   k

v A = v B + v A / B

Onde v A / B = ω A B × r A / B

Observando que v A / B é perpendicular a r A / B , obtemos r B / A ∙ v B / A = 0    

Formando r A / B ∙ v A , nos temos r B / A ∙ v A = r A / B ∙ ( v B + v A / B )

= r A / B ∙ v B + r A / B ∙ v A / B ou r A / B ∙ v A = r A / B ∙ v B

Passo 3

Da equação:

- 0.175 i + 0.15   j + 0.15   k ∙ v A   k

= - 0.175   i + 0.15   j + 0.15   k ∙ - 0.18   i   0.15   v A = ( - 0.175 ) ( - 0.18 )

Ou v A = 0.21   m / s   v A = ( 0.21   m / s ) k

Velocidade relativa: v A / B = v A - v B

= ( 0.18   m / s ) i + ( 0.21   m / s ) k

v A / B ∙ v A / B = ( 0.18   m / s ) ² + ( 0.21   m / s ) ²

= 0.0765   m 2 / s ²

Aceleração do colar B: a B = 0

Aceleração do colar A: a A = α A k

a A = α B + a A / B

Onde a A / B = α A / B × r A / B + ω A B × v A / B

Passo 4

Observando que α A / B × r A / B é perpendicular a r A / B , obtemos r B / A ∙ α A / B × r A / B = 0    

Também observamos que r A / B ∙ ω A B × v A / B = v A / B ∙ r A / B × ω A / B

= - v A / B ∙ v A / B = - ( v A / B ) ²

Então, r A / B ∙ a A / B = 0 - ( v A / B ) ² = - ( v A / B ) ²

Formando r A / B ∙ a A , nos temos r B / A ∙ a A = r A / B ∙ ( a A + a A / B )

= r B / A ∙ a B + r A / B ∙ a A / B ou r A / B ∙ a A = r A / B ∙ a B - ( v A / B ) ²

Formando equação: - 0.175 i + 0.15 j + 0.15 k ∙   α A k = 0 - 0.0765

0.15 α B = 0.0765                           α B = 0.51   m / s ²      

Resposta

a B = - ( 510   m m / s ² ) k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 16.7, considerando que as rodinhas estão travadas e que escorregam no piso áspero ( μ = 0,25 ) .
A empilhadeira mostrada na figura tem a massa de 1,125 k g e é usada para elevar um caixote de massa m = 1,250 k g . Sabendo que a empilhadeira está em repouso, determine (a) a aceleração para cima pa
Uma placa retangular uniforme tem massa de 5 k g e é mantida na posição por três cordas mostrado na figura. Determine o maior valor de θ para que ambas nas cordas AD e BE permaneçam esticadas imediata
Resolva o Problema 16.11, considerando que a aceleração a do suporte é dirigida para baixo.
Considerando que a massa de um barril cheio somado com seu conteúdo tem uma massa combinada de 100 k g . Um cilindro C é ligado ao barril na altura h = 550 m m como mostra figura. Sabendo que μ s = 0,