Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 118
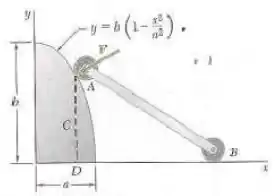
À medida que rola ao longo da superfície do elemento , o rolete seguidor exerce uma força constante perpendicular à superfície. Substitua por um sistema força-binário equivalente no ponto obtido traçando-se a perpendicular desde o ponto de contato até o eixo . Para e , determine o valor de para o qual o momento do sistema força-binário equivalente em é máximo.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiro, vamos encontrar o valor de , que é a inclinação da reta tangente ao elemento .
Como é descrito pela equação:
Temos que a inclinação é dada por:
Agora, podemos aplicar uma coisa interessante. Como é perpendicular à superfície, temos que:
Onde é o ângulo formado entre a força e a horizontal. Logo:
Passo 2
Podemos então fazer a seguinte relação:
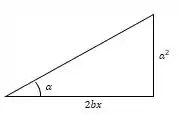
Chamando a hipotenusa de , temos que:
E portanto:
Pronto... Fizemos isso tudo porque queremos encontrar o binário resultante em . Vamos calcular no próximo passo.
Passo 3
Sabemos que a força equivalente que atua em é , o momento equivalente é dado por:
Podemos retratar por , portanto:
Distribuindo as variáveis, temos:
Portanto, o sistema força binário é dado por:
E:
Passo 4
Item b:
Agora queremos o onde o momento do sistema força binário em é máximo.
Primeiro, vamos substituir os valores dados. Para e , temos que:
Bom... Sabemos que para que , seja máximo a sua derivada com relação a deve ser nula, portanto:
Aplicando a regra do quociente para derivação, encontraremos o seguinte resultado:
Resolvendo para , temos:
Como estamos trabalhando com direções o deve ser positivo, portanto:
E: