Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 144

Um membro de seção transversal retangular submetido à compressão, tem comprimento efetivo de 915mm e é feito da liga de alumínio 2014-T6, para a qual a tensão admissível é de 165 MPa. Usando o método da interação, determinar a menor dimensão d da seção transversal que pode ser usada, quando e = 10mm.

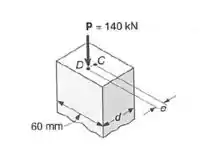
Passo 1

E ai gurizada vamos começar trazendo os dados do enunciado, partiu???

A = 56 d       c = 1 2 d   e = 10 m m   L e = 915 m m

σ μ , b = 165 M P a       P = 140   k N

I x = 1 12 56 d 3                   r x = d 12

Passo 2

Vamos então assumir algumas relações, vem comigo :D

Assuma r x = r m i n     ,     i . e .   d < 60 m m

L e r m i n = 12 L e / d  

Assuma L e r m i n >55. σ μ , c = 372 × 10 3 L e r x 2 = 37200 d 2 12 L e 2 = 372000 12 915 2 d 2 = 0,037 d 2

P A σ μ , c + P e c I σ μ , b = 140000 56 d 37000 d 2 + 12 140000 10 1 2 d 56 d 3 165 = 1

60659 d 3 + 844,2 d 2 = 1           L e t x = 1 d       60659 x 3 + 844,2 x 2 = 1  

Passo 3

Temos então agora que resolver para x, x = 0,02107 ,        

  d = 1 d = 47,46 < 56 m m

L r x = ( 12 ) ( 915 ) / 47,46 ) = 67,21 > 55                        

d = 47,5 m m

Ufaaa encontramos nosso diâmetro :D

Resposta

47,5 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

W 150 × 18 que está livre no topo C e engastada na base B. Sabendo que a excentricidade da força é e = 6 m m , determine o maior comprimento admissível L se a tensão admissível na coluna for 80Mpa. Us
Resolva o problema 10.55 considerando que e = 16 m m e P = 155 k N .
σ E = 250 Mpa e E = 200 GPa, determine o coeficiente de segurança em relação ao escoamento. (Sugestão: Como o coeficiente de segurança deve ser aplicado à força P, não às tensões, use a figura para de
P = 220 k N é aplicada a um ponto localizado no eixo x a uma distância e = 6 m m do eixo geométrico da coluna de mesa larga BC. Sabendo que E = 200 G P a , escolha o perfil W 200 mais leve que possa s
Resolva o Problema 10.51 considerando que a intensidade da força axial seja P=345kN. P = 220 k N é aplicada a um ponto localizado no eixo x a uma distância e = 6 m m do eixo geométrico da coluna de me