Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 21
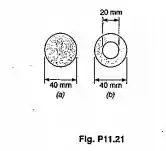
Um membro em compressão, de comprimento efetivo igual a 2m consiste de uma barra maciça de latão, de diâmetro igual a 40mm. Para reduzir de 25% o peso do membro, a barra maciça é substituída por uma barra vazada de seção transversal, como mostrado. Determinar: (a) a porcentagem de redução da carga crítica;(b) o valor da carga crítica para a barra vazada. Usar E=105GPa
Passo 1
Fala meu povo, tudo certinho?
Bom temos duas situações aqui, uma seção maciça antes e uma vazada, o item a nos pede a porcentagem que a carga crítica se reduz, para tal vamos calcular para as duas colunas a carga crítica e fazer uma relação usando:
E daqui faremos:
Como as duas barras vão possuir o mesmo comprimento e mesmo módulo de elasticidade basicamente a relação entre as cargas críticas é a relação entre seus momentos de inércia. A redução enfim vai ser o total menos a relação encontrada que em termos de porcentagem vamos escrever:
Onde as grandezas que tem 1 como índice são da seção maciça e as quais possuem 2 são da seção vazada.
Passo 2
Inicialmente o momento de inércia da seção maciça é:
E para a seção vazada a gente tem:
Lembrando que a coluna circular tem a mesma resistência para cada eixo, daí a gente substitui os valores e:
Voltando a relação apresentada a gente vai ter:
E substituindo:
Passo 3
Agora o item b, nos pede a carga crítica da seção vazada, a gente pode calcular da seção cheia e reduzir ou ir direto pelo cálculo da vazada. Como já temos o momento de inércia da seção vazada vale fazer o cálculo direto mas você pode fazer como preferir.
A carga crítica vai ser dada por:
Substituindo geral a gente vai ter:
E aí resolvemos nosso item b.