Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 34
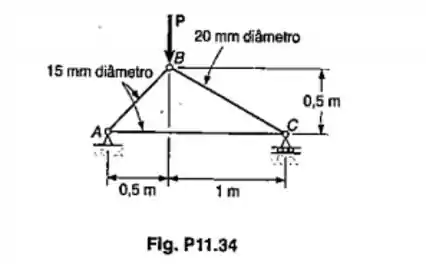
Sabendo-se que um coeficiente de segurança de 2,6 é desejado determinar a maior carga P que pode ser aplicada a estrutura mostrada. Usar E=200GPa e considerar somente flambagem no plano da estrutura.
Passo 1
Fala aí, bora resolver mais uma questão topzinha?
Aqui o nosso pensamento deve ser o seguinte, aquela carga P não é a causadora direta da flambagem, as reações nos apoios é que serão responsáveis e vale lembrar que somente esforços de compressão, sendo assim vamos fazer um diagrama de corpo livre e olhar onde pode acontecer cada esforço.
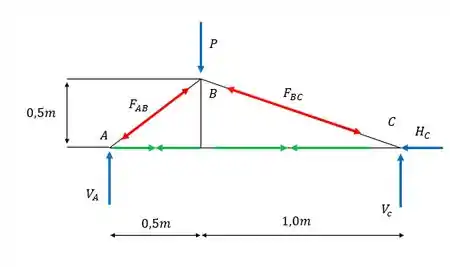
A dica pra fazer esse desenho é sempre desenhar duas setinhas saindo do meio de cada barra combatendo um esforço externo ou de outra barra e no fim, as ações devem se anular. De vermelho são as quais estão comprimidas e as de verde são as tracionadas, e para flambagem somente as comprimidas nos interessam, a partir daqui vamos relacionar os esforços de cada barra com o peso P e considerar que eles são o peso admissível que resistem com segurança a flambagem. Lembrando que do fator de segurança a gente tem a relação.
E que pro peso crítico é dado por:
Passo 2
Vamos agora encontrar os esforços de compressão nas barras mas antes precisamos das reações de apoio.
Pelo somatório das forças externas a gente vê que:
E:
Se a gente pegar o ponto A como referência e calcular o somatório dos momentos fletores poderemos ver que para o sentido horário negativo temos:
Voltando na equação dos esforços verticais a gente substitui :
Beleza, agora que encontramos as reações bora partir pro calculo das forças de compressão que podem causar flambagem, com a figura do DCL a gente pode observar que fazendo Pitágoras que:
E por semelhança a gente pode calcular da seguinte forma:
Rearrumando temos:
E para a outra barra comprimida, também por Pitágoras encontramos seu comprimento.
E da mesma forma por semelhança:
Passo 3
Maneiro, calculamos os esforços em cada barra, mas e aí? Bom pra que a estrutura resista a flambagem com aquele fator de segurança essa relação precisa ser satisfeita:
porém teremos que avaliar para ambas as barras e encontrar o menor valor de P para que o esforço não seja maior que o admissível.
Lembrando que:
Sendo assim:
E como a seção é circular temos:
E aí:
Sendo assim temos:
E como calculamos:
E enfim:
Passo 4
A outra possibilidade que temos de avaliar é a barra BC:
Lembrando que:
Sendo assim:
E precisamos do momento de inércia da barra que é:
E enfim nos dá:
Enfim com o valor relacionado a P que tiramos no passo 2, temos:
Substituindo e isolando P:
Entre os dois, ficamos com o menor valor que é o valor limite para esse fator de segurança: