Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 16
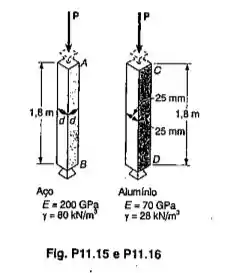
Determinar a dimensão d para que a coluna de aluminío e de aço tenham o mesmo peso e, calcule a carga crítica para cada uma das colunas
Passo 1
Fala meu povo, tudo certo? Vamos devagarzinho resolvendo passo a passo, nossa primeira meta é relacionar os pesos da coluna e encontrar as dimensões da coluna de aço para calcular o momento de inércia que vai nos levar ao peso crítico dela, lembrando que o peso é dado por.
E com cada peso específico:
Após isso encontraremos o peso crítico para cada coluna usando:
Na figura do enunciado fica claro que a coluna é bi-rotulada então não há alterações no comprimento efetivo da mesma.
Passo 2
Vamos colocar a fórmula do peso do alumínio aqui.
E o enunciado nos diz que os pesos precisam ser iguais então:
Isolando a área do aço que nos interessa:
Substituindo os valores temos:
E enfim por ser uma coluna quadrada:
E isolando d, temos:
Aqui vale um comentário, o gabarito do livro apresenta resposta do diâmetro como 148mm porém isso não condiz com as outras respostas que poderão ser observadas no desenrolar da questão.
Passo 3
Agora que temos tudo, mãos a obra e vamos começar pela coluna de alumínio.
A coluna de alumínio é quadrada, ou seja, não possui eixo fraco e seu momento de inércia é:
Assim nosso P crítico será, substituindo os valores na fórmula apresentada no passo 1. E detalhe que aqui vale trabalhar com tudo em milímetros e também com gigapascal que é newton/mm², pois assim a gente só precisa converter o comprimento da coluna.
E com:
E aí usamos a equação:
Substituindo temos:
Para o alumínio (a):
Passo 4
A coluna de aço também é quadrada, ou seja, não possui eixo fraco e seu momento de inércia é:
Com:
Daí usamos a equação da cara crítica:
Substituímos os valores na fórmula: