Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 29

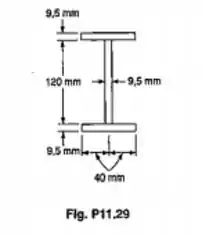
Uma coluna de 6m de comprimento efetivo será feita com três placas, como mostrado. Usando-se E=200GPa, determinar o coeficiente de segurança, em relação a flambagem, para uma carga centrada de 16kN.

Passo 1

Fala meu povo, bora pra mais uma?

Temos aqui uma seção I, composta por 3 placas e a nossa situação é simples precisamos calcular o peso crítico para encontrar o fator de segurança já que:

F S = P C R P A D M

Lembrando que pro peso crítico é dado por:

P C R = π 2 E I L e 2

Aqui precisaremos do momento de inércia que será calculado.

Passo 2

Bom, já aviso pra vocês de cara que esse tipo de seção tem o eixo y como o mais fraco dispensando muitas vezes o cálculo comparativo, por conta das abas é bem mais difícil que o perfil sofra flambagem em torno do eixo x, sendo assim calcularemos o momento de inércia em torno de y.

I y = I y ( a l m a ) + 2 I y ( m e s a )

Aqui vamos ao cálculo de cada um dos momentos de inércia, mas antes vale dar uma olhada na figura da questão ter uma noção das dimensões.

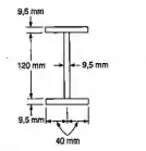
Assim:

I y ( a l m a ) = h b 3 12 = 120 × 9,5 3 12 = 8,57 × 10 3 m m 4

E:

I y ( m e s a ) = h m e s a b m e s a 3 12 = 9,5 × 80 3 12 = 405,33 × 10 3 m m 4

Assim a gente tem:

I y = 8,57 × 10 3 + 2 × 405,33 × 10 3 = 820,66 × 10 3 m m 4

Passo 3

Voltaremos para o nosso querido peso crítico, que agora pode ser calculado já que achamos I.

P C R = π 2 E I L e 2

Substituindo nossa galera aí, temos:

P C R = π 2 × 200 × 820,66 × 10 3 6000 2

E aqui vale lembrar que estamos usando tudo em G P a   e m m , que nos dá o resultado em k N .

P C R = 45 k N

E por fim podemos encontrar o fator de segurança fazendo:

F S = P C R P a d m = 45 16 = 2,81

Resposta

F S = 2,81

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um membro em compressão, de comprimento efetivo igual a 3,6m, é feito soldando-se juntos dois perfis laminados de aço L100X75X6,35mm, como mostrado. Usando-se E=200GPa, determinar a carga centrada adm
Determinar:(a) a carga crítica para a coluna quadrada;(b) o raio da coluna redonda, para que ambas possuam a mesma carga crítica; (c) expressar a área da seção transversal da coluna quadrada como uma
Uma coluna de comprimento efetivo L pode ser confeccionada pregando-se firmemente as pranchas idênticas, tal como mostrado. Para a espessura das pranchas indicadas, determinar a razão entre a carga cr
Um membro em compressão, de comprimento efetivo igual a 3,6m, é feito soldando-se juntos dois perfis laminados de aço L100X75X6,35mm, como mostrado. Usando-se E=200GPa, determinar a carga centrada adm
Uma coluna de aço biarticulada, de 100x100m de seção transversal é apoiada como mostrado no Prob. 11.25. Sabendo-se que inicialmente a força na coluna é zero, determinar o comprimento L necessário, se