Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 91
Determine a força exercida no ramo . Observe que há uma linha horizontal de simetria para as alças, mas não há linha de simetria para as mandíbulas.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força exercida no ramo . É importante destacar que as alças do alicate são simétricas, mas as mandíbulas não.
Então bora resolver! Vamos começar analisando o diagrama de corpo livre da alça que é idêntica à alça , então tudo que fizermos para uma vale para a outra:
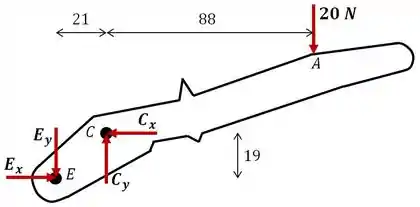
Observe que as forças em e em são reações da força externa vertical de aplicada em . Como não há nenhuma outra força externa aplicada à estrutura, não teremos reações na direção , logo:
Lembrando que o ponto é o mesmo para as duas alças e que o ponto é equivalente ao ponto na alça inferior.
Passo 2
Uma vez que a estrutura está em equilíbrio, os membros separadamente também devem estar. Logo podemos fazer o equilíbrio de momentos em torno de , por exemplo, para encontrar a reação :
E fazendo o equilíbrio de forças na direção vertical temos :
Passo 3
Show! Até aqui bem tranquilo né? Com esse resultado de podemos agora analisar o elemento que, apesar de não ser simétrico ao elemento , eles possuem o ponto em comum onde está aplicada a força . Logo os resultados de que encontrarmos analisando ou devem ser iguais.
Onde a distância é dada por:
Passo 4
Observe que aqui, além da força pedida, temos duas outras incógnitas, as reações e no pino . Para eliminarmos a necessidade de calcular essas reações, vamos fazer o equilíbrio de momentos em torno de para determinar :
Ufa! Essa já foi hein? Partiu pra próxima!
