Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 96
A rampa é usada quando os passageiros embarcam em um pequeno avião de transporte regional. A massa total da rampa e seis passageiros é com centro de massa em . Determine a força no cilindro hidráulico e a magnitude da reação do pino em .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força exercida pelo cilindro hidráulico para elevar a rampa com 6 passageiro e peso total . Pede ainda para determinar reação no pino devido a esse sistema de forças.
Então bora resolver! Vamos começar analisando o diagrama de corpo livre da estrutura separadamente:
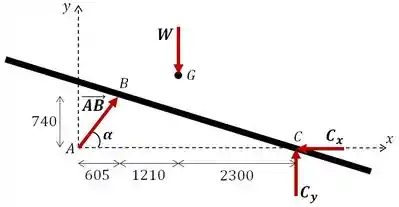
Onde:
E o ângulo do pistão em relação à horizontal é dado por:
Passo 2
Uma vez que a estrutura está em equilíbrio, os membros separadamente também devem estar. Logo podemos fazer o equilíbrio de momentos em torno de , por exemplo, para encontrar a reação do pistão. A escolha desse ponto é estratégica pois inicialmente elimina a necessidade de calcular as reações em .
Passo 3
Show! Agora que nós já temos a força exercida pelo pistão, ainda pela condição de equilíbrio do corpo, podemos fazer o equilíbrio de forças nas direções e para determinar as reações do pino em .
E o módulo da reação nesse pino é:
Até que foi tranquilo né?
Partiu pra próxima!
