Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 55

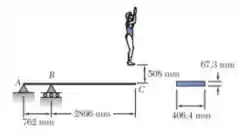
Um mergulhador de peso igual a 711,7 N salta de uma altura de 508mm na extremidade C de um trampolim cuja seção transversal é a mostrada. Considerando que as pernas do mergulhador permanecem rígidas e usando E = 12,4 GPa, determine (a) a máxima tensão normal no trampolim e (c) a carga estática equivalente.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

I = 1 12 16 2,65 3 = 24,813 i n 4

L = 9,5   f t = 114   i n .

a = 2,5   f t = 30   i n .

c = 1 2 2,65 = 1,325   i n .

Sobre a porção AB:

M = - P m L a x

Passo 2

U A B = ∫ 0 a M 2 2 E I d x = P ² m L ² 2 E I a ² ∫ 0 a x 2 d x = P ² m L ² a 6 E I

Sobre a porção BC:

M = - P m v

U B C = ∫ 0 a M 2 2 E I d v = P ² m 2 E I ∫ 0 a v 2 d v = P ² m L ³ 6 E I

Total:

U = U A B + U B C = P m L ² ( a + L ) 6 E I

1 2 P m y m = U m         y m = 2 U m P m = P m L ² ( a + L ) 3 E I

P m = 3 E I L ² ( a + L ) y m = ( 3 ) ( 1,8 × 1 0 6 ( 24,813 ) 114 2 ( 114 + 30 ) y m = 71,598 y m

U m = 1 2 P m y m 35,799 y ² m

Trabalho de peso:

= W h + y m = 160 20 + y m = 3200 + 160 y m

Equacionando:

3200 + 160 y m = 35,799 y ² m  

y 2 m - 4,4694 y m - 89,388 = 0

Passo 3

(a)

y m = 1 2 { 4,4694 + 4,4694 2 + ( 4 ) ( 89,388 ) }

y m = 11,95

(c)

P m = 71,598 11,95 = 856 l b

P m = 856   l b

M m = - 856 114 = 97,535 l b ∙ i n .

(b)

σ m = M m c I = 97,535 1,325 24,813 = 5210   p s i

σ m = 5,21   k s i

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de (a) y m = 11,95 ; (b) σ m = 5,21   k s i e (c) P m = 856   l b .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método do trabalho e da energia, determine a deflexão no ponto D provocada pela força P.
Usando o método do trabalho e da energia, determine a deflexão no ponto D provocada pela força P.
Usando o método do trabalho e da energia, determine a inclinação no ponto D provocada pelo momento M 0 .
Usando o método do trabalho e da energia, determine a inclinação no ponto B provocada pelo momento M 0 .