Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 113

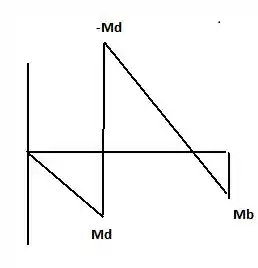
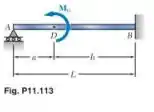
Determine a reação no apoio móvel e trace o diagrama de momento fletor para a estrutura.

Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

O primeiro passo, neste caso, é retirar o apoio em B   e substituí-lo por uma força R B   para cima.

Após isso, vamos listar algumas equações. A energia de deformação é dada por:

U = ∫ 0 L M 2 2 E I d u

Além disso, o deslocamento é dado por:

y A = ∂ U ∂ R A = 0

Ele é nulo porque em A   o apoio impede a deflexão.

Passo 2

Agora, basta substituir. Sabemos que, para A D :

M = R A x

Logo:

∂ U A D ∂ R A = 1 E I ∫ 0 a R A x x d x = R A a 3 3 E I

Para a parte D B :

M = R A x - M 0

Logo:

∂ U D B ∂ R A = 1 E I ∫ a L R A x - M 0 x d x = R A a 3 3 E I = 0

Agora, basta substituir na fórmula do deslocamento:

y A = ∂ U ∂ R A = ∂ U A D ∂ R A + ∂ U D B ∂ R A = 0

Logo, substituindo:

R A = 3 M 0 b L + a 2 L 3

Fazendo o diagrama:

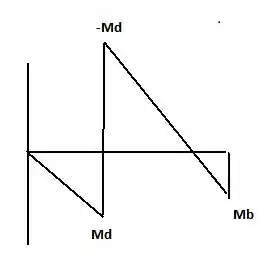
Resposta

R A = 3 M 0 b L + a 2 L 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento indicado, determinar: (a) a declividade no ponto A; (b) a deflexão no ponto C. Usar E = 200 G P a .
Para a viga e o carregamento do Prob. 10,42, determinar a deflexão no ponto A.
Cada um dos membros da treliça mostrada é feita de aço e tem a área da seção transversal indicada. Usando-se E = 200 G P a , determinar a deflexão vertical do nó C.
Cada um dos membros da treliça mostrada é feita de alumínio e tem a área da seção transversal indicada. Usando E = 70 G P a , determinar a deflexão vertical do nó C.
Cada um dos membros da treliça mostrada é feita de alumínio e tem a área da seção transversal indicada. Usando E = 70 G P a , determinar a deflexão horizontal do nó C.