Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 58

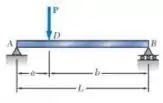
Usando o método do trabalho e da energia, determine a deflexão no ponto D provocada pela força P.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

Reações:

R A = P b L ,       R B = P a L

Sobre AD:

M = R A x = P b x L

U A D = ∫ 0 a M 2 2 E I d x = P ² b ² 2 E I L ² ∫ 0 a x 2 d x

= P ² b ² a ³ 6 E I L ²

Passo 2

Sobre DB:

M = R B x = P b v L

U D B = ∫ 0 a M 2 2 E I d v = P ² a ² 2 E I L ² ∫ 0 a v 2 d v

= P ² b ² a ³ 6 E I L ²

Total:

U = U A B + U B C = P 2 a 2 b 2 a + b 6 E I L ² = P 2 a 2 b 2 6 E I L ²

1 2 P δ D = U                     δ D = 2 U P

δ D = P a 2 b 2 3 E I ↓

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de δ D = P a 2 b 2 3 E I ↓

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11.66 A barra de aço BC com 20mm de diâmetro está fixada na alavanca AB e engastada em C. A alavanca uniforme de aço tem 10mm de espessura e 30mm de largura. Usando o método do trabalho e da energia,
Torques de mesma intensidade T são aplicados aos eixos de aço AB e CD. Utilizando o método do trabalho e energia, determine o comprimento L da porção vazada do eixo CD para que o ângulo de giro em C s
Dois eixos de aço, ambos com diâmetro de 19,1 mm, estão conectados às engrenagens mostradas na figura. Sabendo que G = 77,2 GPa e que o eixo DF está fixo em F, determine o ângulo de rotação da extremi
Para a viga e carregamento mostrados, e usando o teorema de Castigliano, determine a deflexão vertical e horizontal do ponto B .
Três hastes, cada uma com a mesma rigidez E I , são soldadas para formar o pórtico A B C D . Para o carregamento mostrado, determine a deflexão no ponto D .