Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 139
Se o módulo do momento de em relação à linha , determine o módulo de
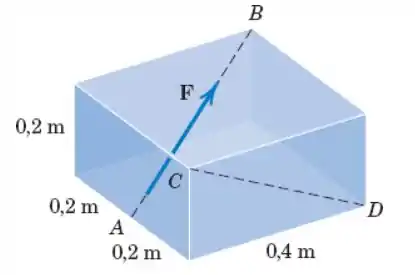
Passo 1
Usamos a fórmula do produto escalar triplo para tentar escrever o módulo do momento em função do módulo da força da seguinte fórmula
Onde é o vetor unitário na direção de , que podemos representar no desenho como sendo
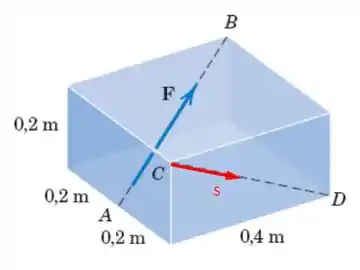
Sendo assim, adotando a aresta que contém como origem do nosso sistema de coordenadas, vamos ter que o nosso vetor será dado por
Passo 2
Vetorialmente, podemos escrever como
Além disso, podemos tomar
Dessa forma, teremos
Pronto, tá resolvido nosso problema.
Resposta
Exercícios de Livros Relacionados
A força F de 1800 N é aplicada à extremidade da viga em H. Expresse F como um vetor, usando os vetores unitários i e j.
A linha de ação da força F de 9,6k N passa pelos pontos A e B , como mostrado na figura. Determine os componentes escalares x e y de F .
O que é um sistema de forças coplanares? Como determinar a resultante desse sistema deforma analítica e em procedimento gráfico?
Em que circunstâncias um sistema de forças aplicado a um corpo tem a tendência de provocar apenas translação? E, em provocar apenas rotação?
Por que, ao caminhar, o pé humano se comporta como uma alavanca inter-resistente? E por que, em uma mordida, o maxilar se comporta como uma alavanca interpotente?