Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.10 - Ex. 17
O que é um sistema de forças coplanares? Como determinar a resultante desse sistema de
forma analítica e em procedimento gráfico?
Passo 1
Boa rapaziada! Tranquilos? Vamos dar seguimentos aos nossos estudos de vetores. E vamos definir de forma bem simples, o que são forças coplanares primeiramente.
Forças coplanares são forças que estão num plano. Então, um sistema de forças coplanares é um conjunto de forças que estão num mesmo plano, mas elas não são atuantes num mesmo ponto.
Vamos desenhar para entender melhor o que foi dito ali.
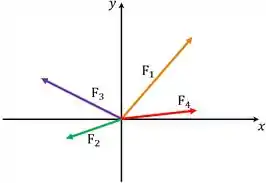
Note que as forças , , e estão no mesmo plano, mas que plano? O plano .
Tranquilo ne? Mas como calculamos a resultante desse role todo? Vamos ver no próximo passo hehe’.
Passo 2
Para calcularmos a resultante, basta somar todos os vetores que estão no mesmo plano. Mas espera, so isso??? Siiiim, só isso, nada de complicado meu jovem padawan. Matematicamente falando seria assim:
Vamos desenhar ne? A somatória de todas as forças é assim que acontece dentro do plano (partindo do nosso exemplo com 4 forças).
Viu só, muito simples!
Resposta
sistema de forças coplanares é um conjunto de forças que estão num mesmo plano, mas elas não são atuantes num mesmo ponto. Soma-se todos os vetores que estão no mesmo plano, gerando a força resultante.