Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 204
O módulo de pouso lunar de com centro de massa tem um raio de giração de em relação a . O módulo é projetado para pousar na superfície lunar com uma velocidade vertical de queda livre de . Se uma das quatro pernas atinge a superfície lunar em cima de uma pequena inclinação sem que sofra um ressalto, calcule a velocidade angular do módulo imediatamente após o impacto enquanto ele gira em torno do ponto de contato. A dimensão de é a distância através da diagonal do quadrado formado pelos quatro pés das extremidades.
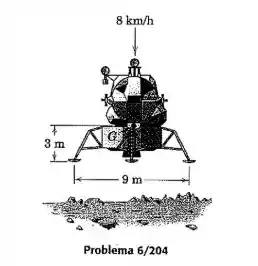
Passo 1
Embora pareça muito complexo, este problema pode ser resolvido a partir da equação da conservação da quantidade de movimento angular, pois .
Antes do impacto, a velocidade do centro de massa é vertical e vale
Passo 2
Aplicando a equação da conservação da quantidade de movimento angular, temos
Simplificando e substituindo os dados da questão, ficamos com
Por fim, resolvendo para , obtemos