Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.8 - Ex. 194
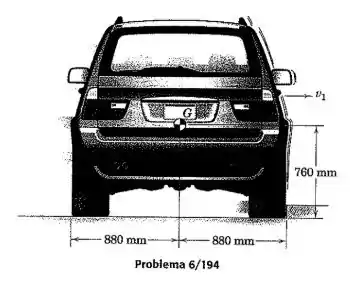
O fenômeno de “tropeço” de um veículo é investigado aqui. O veículo utilitário esportivo está deslizando para o lado com velocidade e sem velocidade angular quando atinge um pequeno meio-fio. Assuma que não ocorre retorno na colisão dos pneus no lado direito e estime a velocidade mínima que fará com que o veículo capote completamente para o seu lado direito. A massa do carro é e seu momento de inércia de massa em relação ao eixo longitudinal através do centro de massa é de .
Passo 1
Considere o estado 1 a condição de deslizamento horizontal do veículo, o estado 2 a partir do instante em que o veículo começa a rotacionar e o estado 3 o instante em que ele capotou completamente para o seu lado direito.
Na ausência de forças externas e impulso angular resultante, temos
Analisaremos a quantidade movimento angular em relação ao ponto de contato entre pneu, meio-fio e asfalto. Assim, ficamos com
Substituindo os dados do problema, obtemos
Passo 2
Do estado 2 para o estado 3, a relação Trabalho-Energia nos indica que
Mas já definimos que no estado 3 o veículo já capotou, portanto ele não possui velocidade. Assim ficamos com
Por fim, resolvendo para , encontramos
Isto é, para o veículo capotará completamente para o seu lado direito.