Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 82

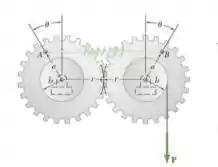
A mola AB, de constante k , está indeformada quando θ = 0 ,   determine (a) os intervalos de θ para equilíbrio estável e (b) dois valores para equilíbrio tal que P é metade do limite superior encontrado em a. Dados   a = 6 0 m m ,   b = 4 5 m m ,   r = 9 0 m m ,   k = 6 k N / m . Determine a estabilidade em cada caso.

Passo 1

Fala aí galera, vamos para mais um problema de estática.

Sabemos que para encontrar a posição de equilíbrio, devemos encontrar a expressão da energia potencial e igualar sua derivada a 0. Logo, sabemos que:

V = 1 2 k x 2

Sabemos que:

x = 2 × a s e n ( θ )

Portanto:

V = 1 2 k 2 a s e n ( θ ) 2

Vamos agora derivar a expressão:

V ' = k 2 a s e n ( θ ) 2 acos ⁡ θ = 4 a 2 k s e n θ c o s ⁡ ( θ )

Para equilíbrio, teremos que os valores satisfazem a equação:

θ = 0

θ = 90

Passo 2

Para determinar a estabilidade, precisamos estudar o sinal da segunda derivada:

V ' ' = 4 a 2 k - s e n 2 θ + c o s 2 θ

Logo, para que a expressão seja positiva (equilíbrio estável), teremos que:

cos ⁡ θ > s e n ( θ )

Portanto:

0 < θ < 45 ;   135 < θ < 180 ;   180 < θ < 225 ; 315 < θ < 360

Resposta

  1. 0 < θ < 45 ;   135 < θ < 180 ;   180 < θ < 225 ; 315 < θ < 360
  2. θ = 0 ;   θ = 90
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro que pesa 75N rola na rampa que faz um ângulo com a hotizontal. Sabendo que k = 5 k N / m e que a mola está indeformada quando x = 0 , determine a distância x para equilíbrio quando β = 6 0 .
Se a mola está indeformada quando seu comprimento vale o raio r , determine o valor do ângulo para equilíbrio se W = 225 N ,r = 225 m m ek = 2,7 k N / m .
A haste AB está presa a uma articulação em A e a duas molas, cada qual de constante k. Se h = 625 mm, d -=300 mm e W = 360 N, determine o intervalo de valores dc k para os quais o equilíbrio da haste
Se uma carga W de 450N é aplicada ao mecanismo em C, sabendo que a mola está indeformada quando θ = 30 , determine o valor de θ para equilíbrio e determine a estabilidade.