Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 108
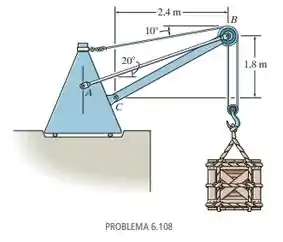
O guindaste de pilar está sujeito à carga com massa de 500 kg. Determine a força desenvolvida na haste de ligação AB e as reações horizontal e vertical no suporte com pino C quando a lança está presa na posição mostrada.
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Primeiramente, sabemos que a caixa pesa como o cabo divide esta força em 2, teremos que a força em cada cabo será de:
Logo, pegando o ponto e aplicando as equações de equilíbrio nele, teremos:
Onde .
Logo:
Continuando com as equações de equilíbrio:
Agora, temos 2 equações e 2 incógnitas. Resolvendo o sistema:
Resposta
Exercícios de Livros Relacionados
Determine a força que o cilindro liso de 20 kg exerce sobre os membros A B e C D B . Além disso, quais são as componentes horizontal e vertical da reação do pino A
A tesoura de poda multiplica a intensidade de corte da lâmina com o mecanismo de alavanca composta. Se uma força de 20 N é aplicada aos punhos, determine a força de corte gerada em A . Considere que a
Determine a força que as garras J do cortador de metal exercem sobre o cabo liso C se forem aplicadas forças de 100 N aos punhos. As garras possuem pinos em E e A , e em D e B . Também há um pino em F
A garra dupla é usada para levantar a viga. Se esta pesa 8k N , determine as componentes horizontal e vertical da força que atua sobre o pino em A e as componentes horizontal e vertical da força que o
A tenaz de dupla garra suporta a bobina com massa de 800 kg e centro de massa em G . Determine as componentes horizontal e vertical das forças que os membros articulados exercem sobre a placa D E I J