Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 161
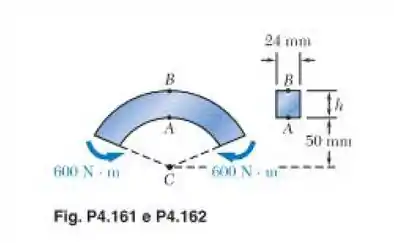
Para a barra curva mostrada na figura, determine a tensão no ponto A quando (a) h = 50 mm e (b) h = 60 mm.
Passo 1
Tá legal! Para a letra (a) vamos começar esse exercício calculando a área da seção transversal da barra curva, que será:
Agora, conforme vimos da Fig. 4.61 dessa seção, para a seção retangular, podemos encontrar o raio de superfície neutra através de:
Onde é o raio externo e é o raio interno. Dessa forma, substituindo os valores conhecidos para essa equação, chegamos em:
Passo 2
Agora vamos calcular a excentricidade, que é a distância entre o centroide e o eixo neutro da seção transversal, dessa forma, teremos:
Substituindo os valores conhecidos, teremos:
Agora podemos encontrar a tensão no ponto A através da equação 4.71, dada por:
Substituindo os valores conhecidos, chegamos em:
Passo 3
Para a letra (b), vamos repetir os cálculos feitos nos passos 1 e 2, só que agora com h = 60 mm, então teremos para a seção transversal:
Agora, o raio de superfície neutra será:
Com isso, podemos calcular a excentricidade, que será:
Por fim, podemos encontrar a tensão no ponto A: