Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 148c
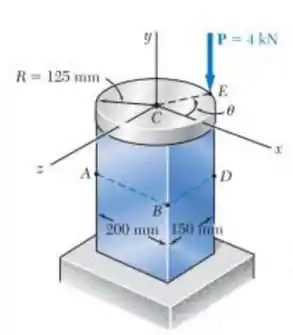
Uma placa rígida circular com raio de está presa a um poste retangular cheio de , com o centro da placa alinhado ao centro do poste. Se uma força for aplicada a E com . Determine:
c) O ponto em que a linha neutra intercepta a linha ABD
Passo 1
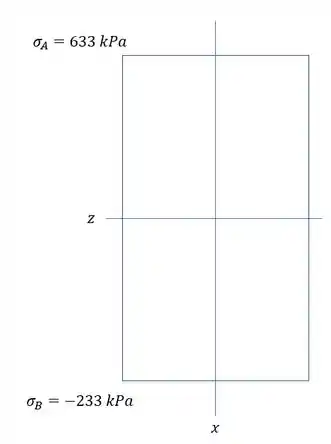
Pelo item A e B já sabemos que as tensões no ponto A e B são dadas por:
Porém precisamos da tensão no ponto D e C para sabermos por onde a LN passa. Assim vamos calcular primeiro essas tensões.
Passo 2
Para determinação de tensões em elementos que estão sujeitos a momentos fletores inclinados, ou ainda, momentos fletores oblíquos, ou momentos fletores assimétricos, temos a seguinte fórmula:
Em que:
Primeiro temos que determinar os momentos em cada uma das direções, ou seja, vamos abrir os momentos fletores em cada uma das direções, e depois analisamos cada uma das direções, sendo assim teremos que:
Decompondo os momentos fletores teremos que:
Sabemos que os momentos são dados por:
Agora que já temos os momentos fletores em cada direção, podemos analisar cada uma delas separadamente.
Passo 3
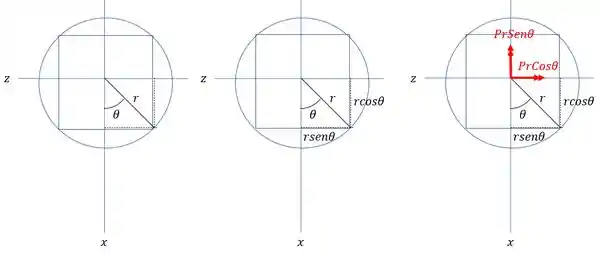
Se definirmos a seção dessa seguinte maneira:
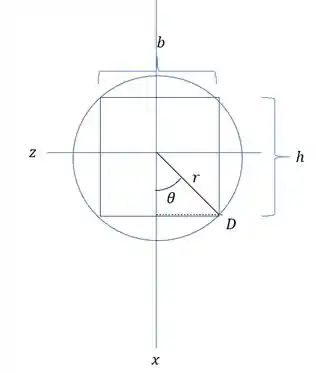
Teremos que:
Como queremos a tensão em D, precisamos das coordenadas X e Z do ponto D, sendo assim teremos que:
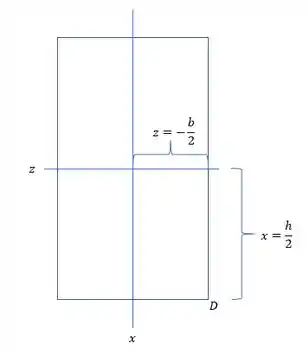
Substituindo nas tensões teremos que:
Substituindo teremos que:
Como queremos a tensão em C, precisamos das coordenadas X e Z do ponto C, sendo assim teremos que:
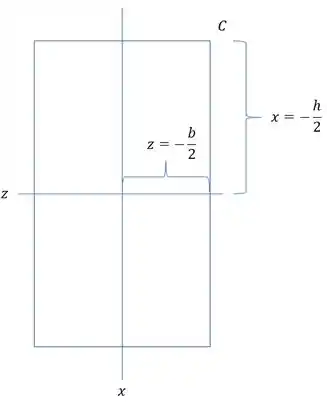
Substituindo nas tensões teremos que:
Substituindo teremos que:
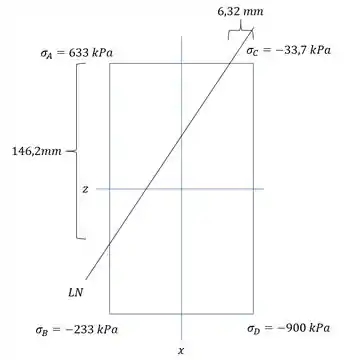
Assim temos que todas as tensões que agem são dadas por:
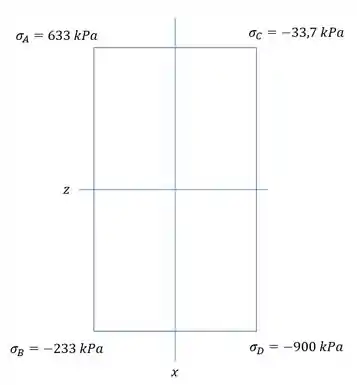
Agora podemos ver a LN passando nas faces em que temos uma diferença entre sinais.
Passo 4
Olhando a face com a reta AB e desenhando o diagrama, teremos que:
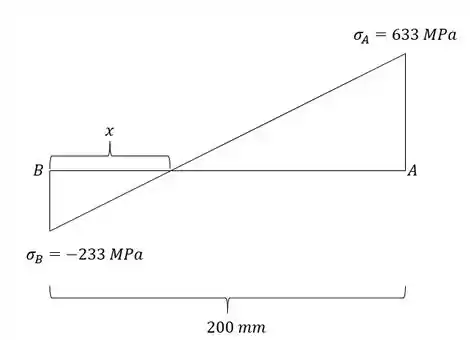
E a distância com relação a A é dado por:
Olhando a face com a reta AC e desenhando o diagrama, teremos que:
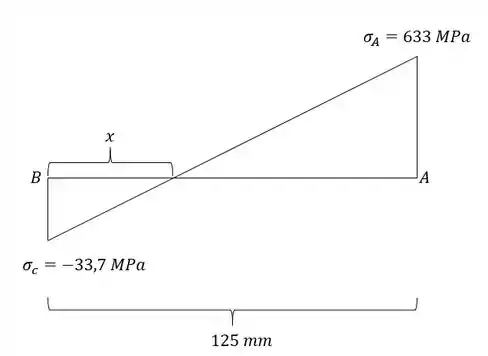
Assim a LN será:
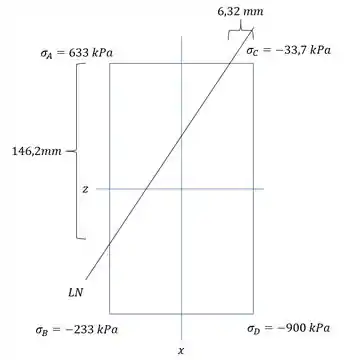
Resposta
