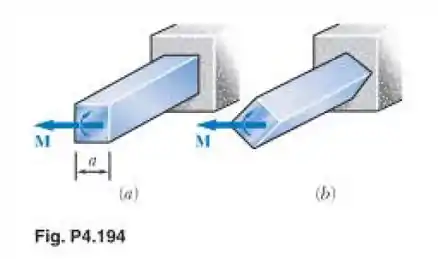
Um momento fletor de intensidade M é aplicado a uma barra quadrada de lado a. Para cada uma das orientações mostradas, determine a tensão máxima e a curvatura da barra.

E, nós sabemos que a tensão máxima para um momento fletor é dado por:

Substituindo as expressões encontradas, chegaremos em:

Agora vamos encontrar o raio de curvatura da barra para a configuração da letra (a), sabendo que o raio de curvatura pode ser encontrado através de:

Substituindo a expressão encontrada para o momento de inércia e isolando o raio de curvatura, teremos:

Agora para a letra (b), vamos ter que dividir a seção quadrada em dois triângulos, para que possamos calcular o momento de inércia total da seção. Dividindo a seção em 2 e colocando o eixo de referência no centro, teremos:

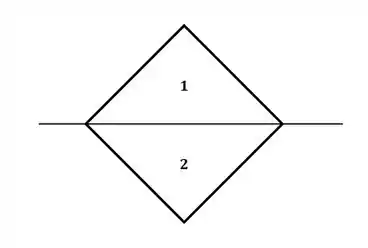
Agora, nós sabemos que para um quadrado de lado , sua diagonal terá comprimento de:

Sendo assim, para as duas seções da figura acima, a base dos triângulos será exatamente a diagonal do quadrado, ou seja:

E a sua altura será metade da diagonal, ou seja:

Com isso, podemos calcular o momento de inércia da seção 1, lembrando que o momento de inércia para um triângulo com relação a sua base é dado por:

Substituindo os valores conhecidos, temos:

Beleza, devido a simetria da seção, o momento de inércia da região 2 será igual ao da região 1, ou seja:

Então, o momento de inércia total da seção será:

Com isso podemos encontrar a tensão máxima nessa seção, lembrando que a distância da linha neutra até a extremidade corresponde à metade da altura, ou seja, metade da diagonal do quadrado, então teremos:

Então, a tensão máxima será:

Substituindo os valores conhecidos, temos:

E, por sua vez, o raio de curvatura será:

Substituindo a expressão para o momento de inércia para a seção e isolando o raio de curvatura, teremos: