Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas de Revisão - Ex. 192

Duas forças verticais são aplicadas à viga com a seção transversal mostrada na figura. Determine as tensões de tração e de compressão máximas na parte BC da viga.

Passo 1

Tá legal! A primeira coisa que devemos fazer nesse exercício é dividir a seção transversal da viga em 2 partes, onde teremos:

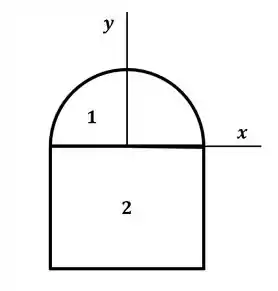
Agora, com a seção dividida, vamos calcular as propriedades de cada uma delas. Começando pela seção 1, podemos escrever sua área como sendo metade da área de um círculo, onde temos:

A 1 = π d 2 4 2 = π 0,05 2 4 2 → A 1 = 981,75.10 - 6   m 2

Agora, vamos determinar a localização do seu centroide. Sabendo que o centroide de um semi círculo é dado por:

y - = 4 r 3 π

Substituindo os valores conhecidos, teremos:

y - 1 = 4 0,025 3 π → y - 1 = 10,61.10 - 3   m

Agora vamos refazer os cálculos para a seção 2. Começando pela área, temos:

A 2 = b h = 0,05 0,025 → A 2 = 1,25.10 - 3   m 2

E o seu centroide será:

y - 2 = - h 2 - 0,025 2 → y - 2 = - 0,0125   m

Passo 2

Agora podemos encontrar a localização do centroide da seção através de:

y - = ∑ A i y - i ∑ A i

Substituindo os valores que encontramos lá no passo 1, teremos:

y - = 981,75.10 - 6 10,61.10 - 3 + 1,25.10 - 3 - 0,0125 981,75.10 - 6 + 1,25.10 - 3 → y - = - 2,3339.10 - 3   m

Agora vamos calcular o momento de inércia da área 1 com relação ao centroide. Lembrando que precisamos usar o teorema dos eixos paralelos nesse caso, onde temos:

I = I - + A d 2

Para a seção 1, essa equação se torna:

I 1 = I - 1 + A 1 d 1 2

Lembrando que o momento de inércia de um semi-círculo é dado por:

I = π r 4 8 - A y - 2

A equação para o momento de inércia da seção 1 se torna:

I 1 = π r 4 8 - A 1 y - 1 2 + A 1 y - 1 - y - 2

Substituindo os valores conhecidos, teremos:

I 1 = π 0,025 4 8 - 981,75.10 - 6 10,61.10 - 3 2 + 981,75.10 - 6 10,61.10 - 3 - - 2,3339.10 - 3 2

I 1 = 207,35.10 - 9   m 4

Passo 3

Agora vamos calcular o momento de inércia para a seção 2,

I 2 = I - 2 + A 2 d 2 2

Lembrando que o momento de inércia de uma seção retangular é dada por:

I = b h 3 12

A equação para o momento de inércia da seção 2 se torna:

I 2 = b h 3 12 + A 2 y - 2 - y - 2

Substituindo os valores conhecidos, chegamos em:

I 2 = 0,05 0,025 3 12 + 1,25.10 - 3 - 0,0125 - - 2,3339.10 - 3 2

I 2 = 194,29.10 - 9   m 4

Sendo assim, o momento de inércia total da seção será:

I = I 1 + I 2 = 207,35.10 - 9 + 194,29.10 - 9 → I = 401,64.10 - 9   m 4

Beleza! Agora que temos as informações que precisamos sobre a seção transversal da viga. Nós sabemos que as maiores tensões ocorrerão nas extremidades inferior e superior da mesma. Dessa forma, vamos calcular a distância do centroide da seção até o topo e até a extremidade inferior da viga. Começando pelo topo, temos:

y t o p o = 0,025 + y - = 0,025 + 2,334.10 - 3 → y t o p o = 27,334.10 - 3   m

E a distância do centroide até a parte inferior será:

y i n f = - 0,025 + y - = - 0,025 + 2,334.10 - 3 → y i n f = - 22,666.10 - 3   m

Passo 4

Agora vamos calcular o momento resultante gerado pelas forças aplicadas a viga. Considerando o ponto C, que será o ponto de maior momento, teremos:

M = P d C

Substituindo os valores conhecidos, temos:

M = 4000 0,3 → M = 1200   N . m

Agora então podemos utilizar a equação 4.16 vista nesse capítulo para encontrar a tensão gerada pelo momento. Então, começando pela tensão no topo, teremos:

σ t o p o = - M y t o p o I

Substituindo os valores conhecidos, teremos:

σ t o p o = - 1200 27,334.10 - 3 401,64.10 - 9 → σ t o p o = - 81,67   M P a

Agora, utilizando novamente a equação 4.16 para calcular a tensão na parte inferior, teremos:

σ i n f = - M y i n f I

Substituindo os valores conhecidos, teremos:

σ i n f = - 1200 - 22,666.10 - 3 401,64.10 - 9 → σ i n f = 67,72   M P a

Resposta

σ t o p o = - 81,67   M P a

σ i n f = 67,72   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra está sujeita a um momento fletor M = 17,5 N.m. Se r = 5 mm, determine a tensão de flexão máxima no material.
A barra tem espessura de 6,25 mm e é feita de um material com tensão de flexão admissível σadm = 126 MPa. Determine o momento máximo M que pode ser aplicado.
Se o raio de cada entalhe na chapa for r = 10 mm, determine o maior momento M que pode ser aplicado. A tensão de flexão admissível para o material é σadm = 180 MPa.
A barra está sujeita a um momento M = 20 N.m. Determine a tensão de flexão máxima na barra e trace um rascunho que mostre, aproximadamente, a variação da tensão na seção crítica.
A barra entalhada simplesmente apoiada é submetida a duas forças P. Determine o maior valor de P que pode ser aplicado sem provocar o escoamento do material. O material é aço A-36. Cada entalhe tem ra