Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas de Revisão - Ex. 196

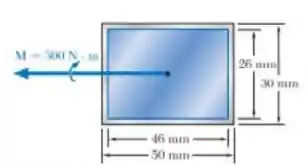
Com o objetivo de incrementar a resistência à corrosão, um revestimento de alumínio com espessura de 2   m m foi aplicado à barra de aço mostrada. O módulo de elasticidade é de 200   G P a para o aço e de 70   G P a para o alumínio. Para um momento de flexão de 300   N ∙ m , determine ( a ) a tensão máxima no aço, ( b ) a tensão máxima no aluminío,   ( c ) o raio de curvatura da barra.

Passo 1

Fala aí pessoal, tudo bem? Bora resolver mais um exercício.

Primeiro, devemos usar o alumínio como material de referência. Para o alumínio temos que:

n = 1

Portanto:

n = E s E a = 200 70 = 2,857

Em seguida, vamos calcular a área das seções transversais. Para o aço, temos que a área da seção é de:

A a ç o = 46 26 A a ç o = 1196   m m 2

Já para obtermos a área da seção alumínio, precisamos diminuir pela área do aço. Logo:

A a l u m í n i o = 50 30 - 1196 A a l u m í n i o = 304   m m 2

Em seguida, vamos calcular o momento de inércia das seções transversais. Ele é dado por:

I = 1 12 b h 3

Então, o momento de inércia do aço vai ser:

I a ç o = 1 12 46 26 3 I a ç o = 67,375   m m 4

E para o momento de inércia do alumínio, temos:

I a l u m í n i o = 1 12 b h 3 - I a ç o I a l u m í n i o = 1 12 50 30 3 - 67,375 I a l u m í n i o = 45,125   m m 4

Assim, o momento de inércia para a seção transformada é dada por:

I = n a ç o I a ç o + n a l u m í n i o I a l u m í n i o I = 2,857 67,375 + 1 45,125 I = 237,615 × 10 - 9   m 4

Passo 2

Agora, vamos determinar a tensão máxima no aço. Sabemos que ela é dada por:

σ a ç o = n a ç o M y a ç o I

Já sabemos o momento de flexão, dado no enunciado, o momento de inércia para a seção e o valor de n . Assim, a distância para a linha neutra vai ser:

y a ç o = 26 2 = 13   m m

Logo, substituindo:

σ a ç o = 2,857 300 0,013 237,615 × 10 - 9 σ a ç o = 46,9   M P a

Passo 3

Para encontrarmos a tensão máxima no alumínio, basta repetirmos o passo 2 , só que agora vamos fazer em função da seção de alumínio. Logo:

y a l u m í n i o = 26 2 = 13   m m

Portanto:

σ a l u m í n i o = 1 300 0,015 237,615 × 10 - 9 σ a l u m í n i o = 18,94   M P a

Passo 4

Por fim, sabemos que o raio de curvatura é dado por:

ρ = E I M ρ = 70 × 10 9 237,615 × 10 - 9 300 ρ = 55,4   m

É isso, galera!!! Bora zerar esse livro?

Resposta

σ a ç o = 46,9   M P a

σ a l u m í n i o = 18,94   M P a

ρ = 55,4   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tensão de flexão admissível para a barra é σadm = 175 MPa. Determine o momento máximo M que pode ser aplicado à barra..
A barra prismática AB é feita de uma liga de bronze para a qual a curva tensão-deformação especifica em tração é mostrada na figura. Considerando que a curva de σ em função de ϵ é a mesma em compressã
Determine o momento plástico M P , de uma viga de aço com a seção transversal mostrada, admitindo que o aço é elastoplástico com resistência ao escoamento de 240M P a .
Um pequeno segmento de perfil laminado com seção W 8 × 31 suporta uma placa rígida na qual duas cargas P eQ , são aplicadas conforme mostrado. As deformações nos dois pontos A e B na linha de centro d