Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 107
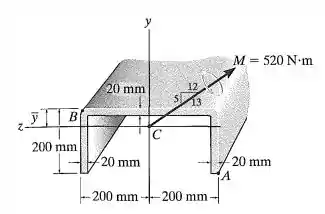
O momento interno resultante que age na seção transversal da escora de alumínio tem valor e está direcionado como mostra a figura. Determine a tensão de flexão máxima na escora. A localização do centroide da área da seção transversal da escora deve ser determinada. Especifique, também, a orientação do eixo neutro.
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat! Precisamos achar a tensão máxima nessa viga aí!
A ideia quando a gente tem uma seção simétrica mas o nosso momento não está em nenhum dos eixos de simetria é que a gente pode decompor o nosso momento em relação a esses eixos. Assim:
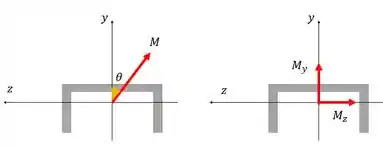
Onde
Aí é usar o prínicipio da superposição para achar a tensão máxima causada por esses dois momentos juntos, calculando as tensões causadas por cada um e somando tudo no final. Vem ver como fica!
Passo 2
Para começar, vamos determinar a posição do centroide da seção transversal. A gente pode dividir nossa seção e posicionar os eixos assim (só agora para achar o centroide):
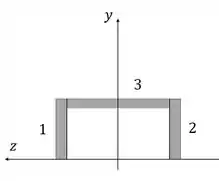
Como 1 e 2 são iguais e tem o mesmo centroide em relação a , a gente só calcula uma delas e multiplica o resultado por 2 ao colocar na fórmula:
E assim, o momento de inércia é dado por:
Podemos repetir o processo para o eixo . Temos:
Passo 3
Agora a gente precisa pensar onde vai ser o ponto de tensão máxima. E para isso, a gente pode ver o efeito dos momentos separadamente. Para entender em que ponto os dois vão causar a maior tensão.
Se a gente representar em azul a área que sofre tração e em amarelo a área que sofre compressão, para cada momento, temos algo assim:
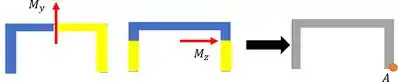
Percebe que a tensão máxima de ocorre na extremidade direita (compressão) ou esquerda (traço) da seção. E para é a extremidade inferior(tração), já que a distância do eixo até a borda é maior nesse caso.
O ponto onde ocorre o valor máximo nos dois casos simultaneamente vai ser o ponto , que vai sofrer compressão.
Então nossa tensão máxima vai estar nele.
Passo 4
Por fim, a tensão de flexão máxima vai ser:
Que é a soma das tensões causadas pelos dois momentos.
O sinais dessas expressões foram escolhidos assim para nossos momentos causem compressão em , como vimos anteriormente.
Ou em compressão.
Passo 5
Para encontrarmos a orientação da linha neutra, temos:
Onde é o ângulo entre e .
Aí a fórmulinha para achar a orientação do eixo neutro é: