Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 101

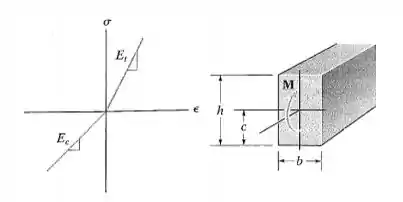
A viga tem seção transversal retangular e está sujeita ao momento fletor M. Se o material de fabricação da viga tiver módulos de elasticidades diferentes para tração e compressão, como mostrado na figura, determine a localização c do eixo neutro e a tensão de compressão máxima na viga.

Passo 1

Primeiramente, sabemos que:

n = E c E t

σ t m á x = n σ c m á x

Logo, substituindo:

M c I = n M h - c I

c = n h - c → c = n h 1 + n

Substituindo o valor de n:

n = E c E t

c = h E c E t + E c

Passo 2

Logo:

σ t m á x = c h - c σ c m á x = h E c E c + E t h - h E c E t + E c

σ c m á x = E c √ E t σ t m á x = E c E t 3 M b h 2 E t + E c E c = 3 M b h ² E t + E c E t

Resposta

c = h E c E t + E c

σ c m á x = 3 M b h ² E t + E c E t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da Seção 5.2 , resolva o Problema 5 . 10 .Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da for
Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da força cortante e momento fletor e ( b ) do momento fletor.
Usando o método da Seção 5.2 , resolva o Problema 5.7 .Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da força
Usando o método da Seção 5.2 , resolva o Problema 5 . 8 .Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da forç
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.