Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 55
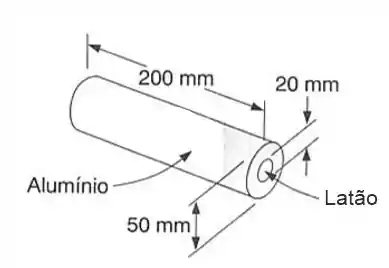
A montagem mostrada consiste em um tubo de alumínio preenchido com núcleo de latão e, com ausência de tensão a uma temperatura de 20°C. Considerando somente deformações axiais, determine a tensão no tubo de alumínio quando a temperatura atingir .
Passo 1
Vamos entender o que acontece quando este tubo é aquecido. A parte de fora (alumínio) dilata mais do que a de dentro (latão), mas como tudo faz parte de uma coisa só a deflexão final terá de ser igual. Então vai ser daí que vai sair o nosso raciocínio, porque ambos estão sujeitos a dilatações térmicas, porém o alumínio vai tracionar o latão enquanto o latão impede a dilatação do alumínio. Em forma de equação vamos ter o seguinte:
Então vamos calcular as deflexões geradas pelas tensões () e pela temperatura ( ) de cada componente e coloca-los nessa equação!
Passo 2
Vamos calcular primeiro as dilatações térmicas. Para o alumínio:
Para o latão:
Passo 3
Agora vamos calcular as deflexões devido às tensões, primeiro para o alumínio:
Calculando a área do alumínio:
Continuando na equação da deflexão
Ainda não temos a força de interação entre as duas partes, de latão e de alumínio.
Calculando a deflexão para o latão:
A área para o latão será de:
Continuando na equação da deflexão
Como dito anteriormente, não temos a força ainda que, por ser a força de interação, é igual para ambos os casos.
Passo 4
Agora vamos substituir na nossa equação do início do problema:
Reorganizando
Passo 5
Para descobrirmos a tensão no alumínio basta dividir a força pela área:
Neste caso a tensão será de compressão, já que o alumínio atrapalha a dilatação do latão. Como é uma tensão compressiva podemos escrever: