Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 34
A viga falhará se o momento fletor máximo em atingir ou a força normal no membro se tornar . Determine a maior carga que ela pode suportar.
Passo 1
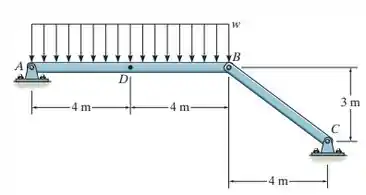
Fala, galera do RespondeAí. Beleza? Bora para mais um exercício de Mecânica. Neste problema, devemos determinar a maior carga que esta viga pode suportar em duas situações. Na primeira, o momento fletor máximo em deve ser menor que .
Portanto, vamos começar esboçando o para a viga , temos:
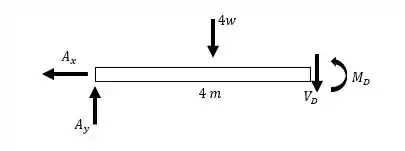
Onde a carga distribuída foi substituída por uma carga concentrada no ponto médio desta viga, ou seja, em . E ela foi encontrada multiplicando a carga pelo comprimento em que ela atua.
Passo 2
Em seguida, utilizar as equações de equilíbrio para determinarmos as reações de apoio:
E também, para o eixo devemos desconsiderar a força cortante, logo:
Com isso, assumindo que o momento fletor máximo ocorre no ponto , temos:
Como o enunciado nos fornece que o momento em é , temos que:
Opa, encontramos o valor máximo da carga para a primeira situação. Bora pra segunda!
Passo 3
No segundo caso, temos que a viga falhará se a força normal no membro se tornar . Com isso, devemos calcular o valor do membro da viga em que a carga seja .
Primeiro, vamos esboçar o DCL:
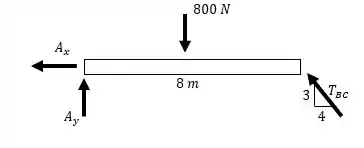
Novamente, a carga distribuída foi substituída por uma carga concentrada no ponto médio desta viga, desta vez, em . E ela foi encontrada multiplicando a carga pelo comprimento em que ela atua.
Passo 4
Como podemos observar no , a tração possui um ângulo relacionado a um triângulo retângulo . Logo, vamos chamar este ângulo de , e então, decompor a força :
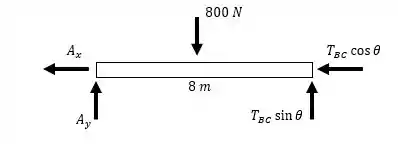
Com isso, vamos determinar a tração do braço a partir da equação do momento no ponto . Fica assim:
Assim, galera, podemos ver que a tração que a gente encontrou é menor que a tração de falha.
Opa, é isso, galera. Bora praticar mais!!!