Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 28
Um motor elétrico exerce um torque de sobre o eixo de alumínio quando está girando com uma velocidade constante. Sabendo-se que e os torques aplicados sobre as polias e são tal como mostrado, determinar o ângulo de torção entre: (a) e ; (b) e .
Passo 1
A questão trata sobre o ângulo de torção, que é definido pela equação:
Onde:
- é o ângulo de torção dado em radianos.
- é a torção
- o momento polar de inércia
- módulo de elasticidade
Pô, se o problema nos deu o módulo de elasticidade, o momento polar de inércia a torção e pede o ângulo então não deve ser algo muito complicado, correto? E sim, realmente não é, só precisamos ficar atentos a uma coisinha, qual torque atua na barra e na barra .
Para isso vamos fazer as seções e descobrir os torque.
Passo 2
A barra não sofre nenhum torque, porque elas está livre para rotacionar, então vamos seccionar a barra :
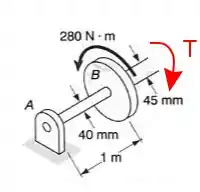
Para que a barra permaneça em equilíbrio deve haver um torque no valor de sendo aplicado na direção oposta, não é mesmo? Esse é o torque mostrado na imagem e que vai entrar na nossa continha:
Passo 3
Vamos calcular o momento polar de inércia rapidinho, lembrado que o raio dessa barra é de
Passo 4
Agora podemos substituir na equação
Para transformar em graus é só multiplicar por
Passo 5
Agora vamos fazer a mesma coisa para a barra e depois é só somar os ângulos! Então vamos seccionar a barra :
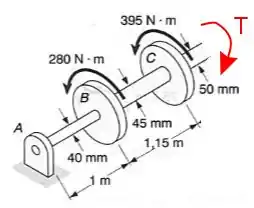
Agora para que a barra permaneça em equilíbrio deve haver um torque T contrapondo os outros dois, ou seja:
Agora vamos substiruir na nossa conta
Passo 6
Vamos calcular o momento polar de inércia rapidinho, lembrado que o raio dessa barra é de
Passo 7
Agora podemos substituir na equação:
Para transformar em graus é só multiplicar por
Passo 8
Somar os dois ângulos:
Resposta
a)
b)