Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 23

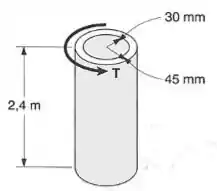
Pede-se determinar: (a) o torque T que causa um ângulo de torção de 3° no eixo cilíndrico vazado de aço ( G = 77   G P a ); (b) o ângulo de torção causado pelo mesmo torque T , num eixo cilíndrico maciço de mesma área de seção transversal.

Passo 1

O problema pede para calcularmos o torque, na letra A, e o ângulod e torção que esse mesmo torque causaria num cilindro maciço. Então vamos lá, a equação que a gente tem que utilizar aqui é essa:

ϕ = T ⋅ L J ⋅ G

Onde:

  • ϕ é o ângulo de torção dado em radianos.
  • T é a torção
  • J o momento polar de inércia
  • G módulo de elasticidade

Passo 2

Aí é só substituir na equação, mas antes vamos calcular o momento de inércia polar J , que para o caso de um cilindro vazado é igual a:

J = π ⋅ c e x t 4 2 - π ⋅ c i n t 4 2

J = π ⋅ 45 × 10 - 3 4 - 35 × 10 - 3 4 2

J = π ⋅ [ 4.100.625 × 10 - 12 - 1.500.625 × 10 - 12 ] 2

J = π ⋅ ( 2.600.000 ) × 10 - 12 2

J = 4.084.070 × 10 - 12 m 4

Passo 3

Passando o ângulo de graus para radiano, temos de multiplicar pelo termo:

2 π 360 °

3 ° = 3 ° ⋅ 2 π   r a d 360 °

3 ° = 0,0523   r a d

Passo 4

Agora podemos fazer a substituição na fórmula

ϕ = T ⋅ L J ⋅ G

T = ϕ ⋅ J ⋅ G L

T = 0,0523 ⋅ 4.084.070 × 10 - 12 ⋅ 77 × 10 9 2,4

T = 0,0523 ⋅ 4.084.070 ⋅ 77 2,4 ⋅ 10 - 12 × 10 9 1

T = 6.860.745 ⋅ 10 - 3   N ⋅ m

T = 6.860 , 745   N ⋅ m

Passo 5

Para resolver a letra B basta calcularmos o novo momento polar de inércia e substituir na equação. Como eles tem a mesma área:

π r 2 = π ( 45 2 - 35 2 )

r 2 = ( 45 2 - 35 2 )

r 2 = 800

r = 28,28   m m

Calculando o momento polar de inércia

J = π ⋅ ( 28,28 × 10 - 3 ) 4 2

J = π ⋅ 640.000 × 10 - 12 2

J = 1.005.310 × 10 - 12   m 4

Passo 6

Aplicando na equação

ϕ = T ⋅ L J ⋅ G

ϕ = 6.860,745 ⋅ 2,4 1.005.310 × 10 - 12 ⋅ 77 × 10 9    

ϕ = 6.860,745 ⋅ 2,4 1.005.310 ⋅ 77 ⋅ 1 10 - 12 × 10 9    

ϕ = 0,000213 ⋅ 10 3   r a d

ϕ = 0 , 213   r a d

Ou em graus:

2 π   r a d 360 °

ϕ = 0,213   r a d ⋅ 360 ° 2 π   r a d

ϕ = 12,2   °

Resposta

a)

T = 6.860,745   N ⋅ m

b)

ϕ = 12,2   °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste cilíndrica cheia BC de comprimento L = 24i n . é conectada na alavanca rígida AB de comprimento a = 15i n , e no suporte C. Especificações de projeto exigem que o deslocamento de A não exceda
A haste cilíndrica cheia BC de comprimento L = 24i n . é conectada na alavanca rígida AB de comprimento a = 15i n , e no suporte C. Especificações de projeto exigem que o deslocamento de A não exceda
O projeto do sistema de engrenagens e eixo mostrado na figura requer que sejam utilizados eixos de aço de mesmo diâmetro para AB e CD. E necessário também que τ a d m ≤ 60M P a e que o ângulo ϕ D pelo
O motor elétrico aplica um torque de 800 N/m ao eixo de aço ABCD quando a rotação tem velocidade constante. Especificações de projeto requerem que o diâmetro do eixo sejam uniforme entre A e D e que o
Um furo é feito em uma chama de plástico em A através de uma força P de 600 N, aplicada a uma extremidade D da alavanca CD, que está rigidamente conectada ao eixo cilíndrico BC . Especificações do pro