Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 140
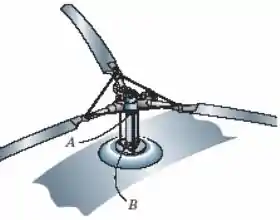
O motor do helicóptero transmite ao eixo do rotor quando a hélice está girando a . Determine, com a aproximação de múltiplo de , o diâmetro do eixo se a tensão de cisalhamento admissível for e as vibrações limitarem o ângulo de torção do eixo a . O eixo tem de comprimento e é feito de aço-ferramenta L2
Passo 1
A questão nos fornece os dados: , e
Por conveniência vamos ajutar a unidade de medida da velocidade
A resolução da questão consiste em identificar qual é o diâmetro necessário para que o eixo resistao ao torque e a deformação.
Então, primeiro vamos usar a fórmula da potência para identificar o torque, e depois a equação da tensão e da deformação por torção para identificar os possíveis diâmetros do eixo.
Passo 2
Calculando o valor do torque aplicado no eixo:
Passo 3
Vamos calcular qual o mínimo diâmetro necessário para resistir a deformação:
Isolamos o momento de inércia:
Substituímos o momento de inércia por sua fórmula:
Isolando o diâmetro:
Passo 4
Agora vamos conferir o diâmetro necessário para resistir ao torque:
Substituíndo a equação do momento de inércia e do raio:
Isolando o diâmetro:
Passo 5
Agora vamo analisar os resultado. Para que o eixo resista ao torque é necessário um diâmetro maior do que o necessário para resistir à deformação. Por isso, para garantir que o eixo resista aos esforços devemos escolher o maior diâmetro.
A questão pede que o diâmetro seja múltiplo de , então aumentamos o eixo até que ele atinja um valor múltiplo.