Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 134
Considere um tubo de parede fina de raio médio e espessura . Mostre que a tensão de cisalhamento máxima no tubo devido a um torque se aproxima da tensão de cisalhamento média calculada pela Equação 5.18 quando .
Passo 1
Em resumo, o questão nos pede pra provar a equação 5.18.
Olhando a figura a baixo, percebemos que na área infinitesima , a tensão de cisalhamento é decorrente de uma certa força . Essa força é resultado do torque aplicado sobre a estrutura.
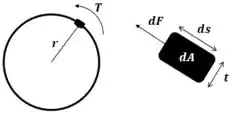
Por isso, precesamos nos lembrar da definição de tensão:
Da definição de torque (torque é igual a força vezes distância):
Substituíndo a primeira na segunda:
Passo 2
Ainda observando a área infinitesimal, percebe-se que ela é aproximadamente quadrada. Então sua área pode ser determinada como:
Passo 3
Vamos agora substituir a equação da área na equação do torque:
E integramos ao redor do caminho para obter o torque:
Se considerarmos que a tensão e a espessura são constantes:
Passo 4
Precisamos determinar o valor da integral de linha acima. Para isso vamos olhar a figura:
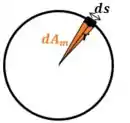
Perceba que o a área em laranja é um triângulo com base e altura . Podemos determinar como:
Podemos substituir a expressão acima na nossa integral:
E fazendo algumas manipulações chegamos na equação 5.18: