Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 61
Se o motor no Problema 17.60 é desengatado do eixo assim que o volante está girando a 15 rad/s, de maneira que M = 0, determine quanto tempo vai levar antes que a resultante da força de atrito do mancal F = 50 N faça o volante parar de girar.
Passo 1
Vamos começar encontrando o valor do momento de inércia do eixo:
Passo 2
Agora, calculando o somatório de momentos em torno do ponto O, conforme figura a seguir, conseguimos encontrar a aceleração angular:
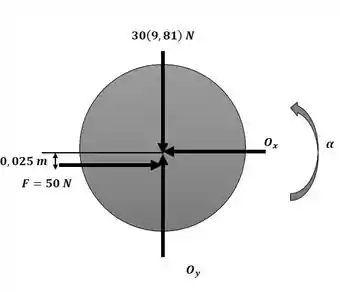
Passo 3
Por fim, aplicando a equação da velocidade angular ao sistema podemos determinar o tempo necessário para que o eixo pare de rodar:
Resposta
Exercícios de Livros Relacionados
O navio tem uma massa de 2 ( 10 6 ) kg e cetro de gravidade em G. dois rebocadores de peso desprezível são usados para virá-lo. Se cada rebocador o empurra com uma força T =10 kN, determine a aceleraç
A placa quadrada de 20 kg está presa por um pino ao anel liso de 5 kg. Determine a aceleração inicial da placa quando P = 100N for aplicada ao anel. A placa está originalmente em repouso.
A placa quadrada de 20 kg está presa por um pino ao anel liso de 5 kg. Determine a aceleração angular inicial da placa quando P = 100 n for aplicada ao anel. A placa está originalmente em repouso.
A bobina tem uma massa de 100 kg e um raio de giração K g=200m m em relação a seu centro de massa G. Se uma força vertical P=200N for aplicada ao cabo, determine a aceleração de G e a aceleração angul
A bobina tem uma massa de 100 kg e um raio de giração K g=200m m em relação a seu centro de massa G. Se uma força vertical P=500N for aplicada ao cabo, determine a aceleração de G e a aceleração angul