Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 117

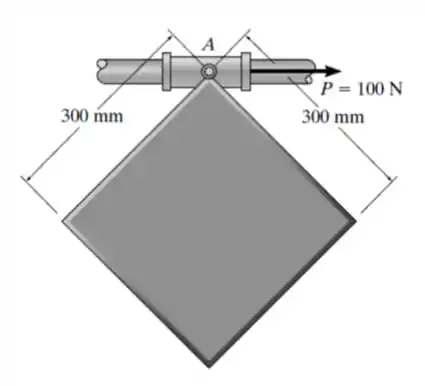
A placa quadrada de 20 kg está presa por um pino ao anel liso de 5 kg. Determine a aceleração inicial da placa quando P = 100N for aplicada ao anel. A placa está originalmente em repouso.

Passo 1

Definir as equações de movimento:

I g =   m ( a 2 + b 2 ) 12 = 20 . ( 0.3 2 + 0.3 2 ) 12 = 0.3 k g . m ²

  ← + Σ F X = m . a g x =   100 = 5 a A + 20 a g x

  ↺ + Σ M A = Σ   μ k A       0 =   20 a g x 0,3 s e n 45 ° -   0,3 a

Passo 2

Aplicando a equação de aceleração relativa temos:

Assim:

a G   =   a A + a   x   r G / a   –   ω ² r G / a    

a g x   i + a g y   j =   a A i + - a k   x   - 0,3 s e n 45 °   j -   0

a g x   i + a g y   j = a A - 0.2121 i

Passo 3

Agrupando por componentes i e j:

a g x = a A - 0.2121 a

a g y   = 0

Substituindo nas equações abaixo:

  1. 100 = 5 a A + 20 a g x

  2. 20 a g x 0,3 s e n 45 ° -   0,3 a

Tem-se:

100 = 5 a A + 20 a A - 0.2121 a

20 a A - 0.2121 . 0,3 s e n 45 ° -   0,3 a = 0

Resolvendo teremos:

a A = 10   m / s ²

a = 35.4   r a d / s ²

a g x = 2,5   m / s ²  

Resposta

Assim a aceleração inicial é   a A = 10   m / s ² .

.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A placa quadrada de 20 kg está presa por um pino ao anel liso de 5 kg. Determine a aceleração angular inicial da placa quando P = 100 n for aplicada ao anel. A placa está originalmente em repouso.
A bobina tem uma massa de 100 kg e um raio de giração K g=200m m em relação a seu centro de massa G. Se uma força vertical P=200N for aplicada ao cabo, determine a aceleração de G e a aceleração angul
A bobina tem uma massa de 100 kg e um raio de giração K g=200m m em relação a seu centro de massa G. Se uma força vertical P=500N for aplicada ao cabo, determine a aceleração de G e a aceleração angul
O cilindro maciço possui um cone do corpo com um semi-ângulo do vértice de 20º. Em um determinado instante a velocidade angular ω tem um módulo de 30 rad/s e está situada no plano y - z . Determine a
O cursor em O e a haste incorporada O C giram em torno do eixo fixo x 0 na taxa constante Ω = 4r a d / s . Simultaneamente, o disco circular gira em torno de O C na taxa constante p = 10r a d / s . De