Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 118

A bobina tem uma massa de 100 kg e um raio de giração K g   =   200   m m em relação a seu centro de massa G. Se uma força vertical P   =   200   N for aplicada ao cabo, determine a aceleração de G e a aceleração angular da bobina. Os coeficientes de atrito cinético e estático entre o trilho e a bobina são μ S   =   0,3 e μ k   =   0,25 , respectivamente.

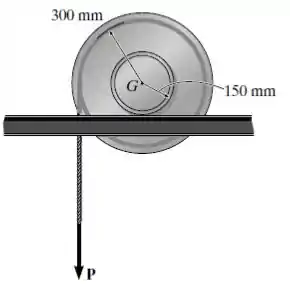
Passo 1

Definir as equações de movimento:

  ← + Σ F X = m . a g x =   F f = 100 a g

  ↑ + Σ F y = m . a g y = N - 100 9,81 -   200 = 0 ; N = 1181   N

  ↺ + Σ M G = I g . a = 200 0,3 -   F f 0,15 =   4 a

Passo 2

Assumindo que não deslizamento:

a g = a . ( 0,15 )

Passo 3

Resolvendo o sistema.

  1. F f = 100 a g

  2. 200 0,3 -   F f 0,15 =   4 a

  3. a g = a . ( 0,15 )

Primeiro deixaremos em termos de a .

F f = 15 . a

Substituindo em F f :

200 0,3 -   15 a 0,15 =   4 a

Isolando para a :

60 =   6,25 a

Então:

a = 9,6   r a d / s

Substituindo:

F f = 15 . a

a g = a . ( 0,15 )

Resposta

Assim a aceleração a g = 1,44   m / s 2 , a força F f = 144   N e a aceleração a = 9,6   r a d / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra esbelta de massa m e comprimento l gira em torno do eixo y como o elemento de um cone circular reto. Se a velocidade angular em torno do eixo y é ω , determine a expressão para a quantidade de
O cone circular reto maciço de massa m , comprimento b , e raio da base r gira a uma velocidade angular p em torno de seu eixo de simetria. Simultaneamente, o suporte e o eixo da haste anexa giram na
A nave espacial mostrada possui uma massa m com centro de massa G . Seu raio de giração em relação a seu eixo z de simetria rotacional é k e em relação a ambos os eixos x ou y é k ' . No espaço, a nav
O cone circular reto de altura h e raio da base r gira em torno de seu eixo de simetria com uma velocidade angular p . Simultaneamente, o cone inteiro gira em torno do eixo x com velocidade angular Ω
A bobina A gira em torno de seu eixo com uma velocidade angular de 20rad/s, inicialmente no sentido de w0 e em seguida no sentido de ws. Simultaneamente, o conjunto gira em torno do eixo vertical com